题目内容
21. (本小题满分12分)
已知函数
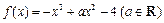 .
.(1) 若函数
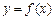 的图象在点P(1,
的图象在点P(1,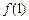 )处的切线的倾斜角为
)处的切线的倾斜角为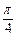 ,求实数a的值;
,求实数a的值;(2) 设
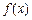 的导函数是
的导函数是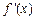 ,在 (1) 的条件下,若
,在 (1) 的条件下,若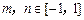 ,求
,求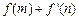 的最小值.
的最小值.(3) 若存在
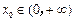 ,使
,使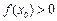 ,求a的取值范围.
,求a的取值范围. ,
,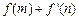 的最小值为 – 11
的最小值为 – 11
解:(1)  ,据题意
,据题意
∴ .
.
(2) 由 (1) 知, ,则
,则
∴ 对于 的最小值为
的最小值为
∵ 的对称轴为
的对称轴为 ,且抛物线开口向下,
,且抛物线开口向下,
∴ 的最小值为
的最小值为 中较小的
中较小的
∵
∴ 当 的最小值为 – 7
的最小值为 – 7
当 的最小值为 – 7
的最小值为 – 7
∴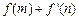 的最小值为 – 11
的最小值为 – 11
(3) ∵
①若 ,当x > 0时,
,当x > 0时, ,
,
∴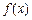 在
在 上单调递减
上单调递减
又 ,则当x > 0时,
,则当x > 0时,
∴ 当 时,不存在x0 > 0,仅
时,不存在x0 > 0,仅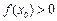
②若a > 0,则当 时,
时,
当 时,
时, ,
,
从而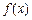 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
∴ 当 时,
时,
据题意, ,∴ a > 3
,∴ a > 3
综上,a的取值范围是 .
.
 ,据题意
,据题意
∴
 .
.(2) 由 (1) 知,
 ,则
,则
| x | – 1 | (– 1,0) | 0 | (0,1) | 1 |
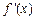 | – 7 | — | 0 | + | 1 |
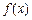 | – 1 | ↘ | – 4 | ↗ | – 3 |
 的最小值为
的最小值为
∵
 的对称轴为
的对称轴为 ,且抛物线开口向下,
,且抛物线开口向下,∴
 的最小值为
的最小值为 中较小的
中较小的∵

∴ 当
 的最小值为 – 7
的最小值为 – 7当
 的最小值为 – 7
的最小值为 – 7∴
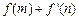 的最小值为 – 11
的最小值为 – 11(3) ∵

①若
 ,当x > 0时,
,当x > 0时, ,
,∴
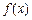 在
在 上单调递减
上单调递减又
 ,则当x > 0时,
,则当x > 0时,
∴ 当
 时,不存在x0 > 0,仅
时,不存在x0 > 0,仅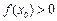
②若a > 0,则当
 时,
时,
当
 时,
时, ,
,从而
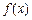 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减∴ 当
 时,
时,
据题意,
 ,∴ a > 3
,∴ a > 3综上,a的取值范围是
 .
.
练习册系列答案
相关题目
 )对称;
)对称;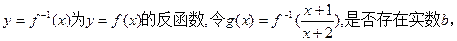 使得任给
使得任给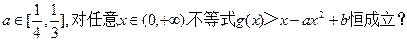 若存在,求b的取值范围;若不存在,说明理由.
若存在,求b的取值范围;若不存在,说明理由.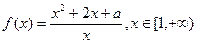 。
。 时,求函数
时,求函数 的最小值;
的最小值; >0恒成立,试求实数
>0恒成立,试求实数 的取值范围。
的取值范围。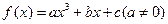 ,
,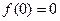 ,其图象在点
,其图象在点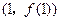 处的切线与直线
处的切线与直线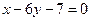 垂直,导函数
垂直,导函数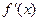 的最小值为
的最小值为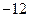 .
.
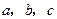 的值;
的值;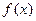 的单调递增区间,并求函数
的单调递增区间,并求函数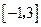 上的最大值和最小值.
上的最大值和最小值. 的图象,给出下列命题:
的图象,给出下列命题: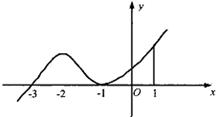
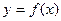 的极值点;
的极值点;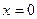 处切线的斜率小于零;
处切线的斜率小于零;
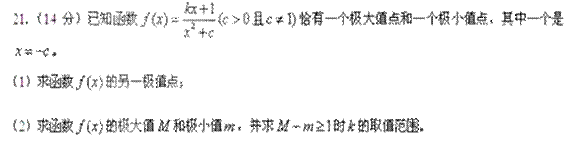
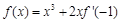 ,则函数
,则函数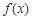 在区间
在区间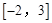 上的值域是( )
上的值域是( )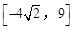
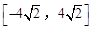
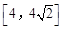
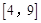
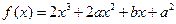 ,
,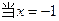 时有极值7,则
时有极值7,则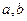 的值分别为 ;
的值分别为 ;