题目内容
已知x1,x2是函数f(x)=2-x-|log2x|的两个零点,则x1•x2的范围是 .
考点:函数的零点与方程根的关系
专题:计算题,函数的性质及应用
分析:作出y=|log2x|和y=2-x在R上的图象,可知恰有两个交点,设零点为x1,x2且|log2x1|>|log2x2|,再结合零点存在定理,可得结论.
解答:
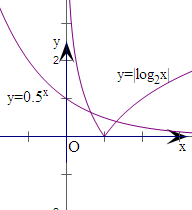 解:令f(x)=0,则|log2x|=2-x,
解:令f(x)=0,则|log2x|=2-x,
作出y=|log2x|和y=2-x在R上的图象,
可知恰有两个交点,设零点为x1,x2且|log2x1|>|log2x2|,x1<1,x2>1,故有
>x2,即x1x2<1.
又f(
)<0,f(1)>0,
∴
<x1<1,∴x1x2>
.
故答案为:(
,1).
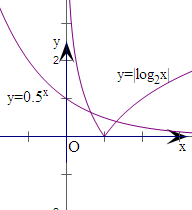 解:令f(x)=0,则|log2x|=2-x,
解:令f(x)=0,则|log2x|=2-x,作出y=|log2x|和y=2-x在R上的图象,
可知恰有两个交点,设零点为x1,x2且|log2x1|>|log2x2|,x1<1,x2>1,故有
| 1 |
| x1 |
又f(
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查函数的零点与方程根的关系,考查数形结合的数学思想,考查学生分析解决问题的能力,正确作出函数图象是关键.

练习册系列答案
相关题目
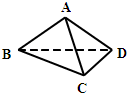 如图,四面体A-BCD中,AB=AD=CD=1,BD=
如图,四面体A-BCD中,AB=AD=CD=1,BD=| 2 |
A、
| ||||
| B、3π | ||||
C、
| ||||
| D、2π |
用5,6,7,8,9组成没有重复数字的五位数,其中个位和万位都是偶数的五位数的个数是( )
| A、36 | B、48 | C、72 | D、12 |
阅读如图所示的程序框图,若输入的N=200,则输出的结果为( )


| A、101 | B、200 |
| C、100 | D、201 |