题目内容
5．△ABC中，$AB=\sqrt{2}$，BC=2，$sinA=\frac{{\sqrt{14}}}{4}$，则sinC=（ ）| A． | $\frac{{\sqrt{3}}}{4}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{7}}}{4}$ | D． | $\frac{{\sqrt{7}}}{3}$ |
分析 由已知利用正弦定理即可计算求值．
解答 解：∵$AB=\sqrt{2}$，BC=2，$sinA=\frac{{\sqrt{14}}}{4}$，
∴利用正弦定理可得：sinC=$\frac{ABsinA}{BC}$=$\frac{\sqrt{2}×\frac{\sqrt{14}}{4}}{2}$=$\frac{\sqrt{7}}{4}$．
故选：C．
点评 本题主要考查了正弦定理在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
1．在数列{an}中，a1=$\frac{1}{2}$，a2=$\frac{1}{3}$，anan+2=1，则a2016+a2017=（ ）
| A． | $\frac{5}{6}$ | B． | $\frac{7}{3}$ | C． | $\frac{7}{2}$ | D． | 5 |
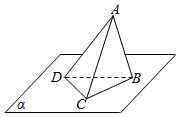如右图，三棱锥A-BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=2，AD=$\sqrt{6}$，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D两点所经过的路程之和是$\sqrt{3}π$．