题目内容
已知A1,A2分别为椭圆 的左右顶点,椭圆C上异于A1,A2的点P恒满足
的左右顶点,椭圆C上异于A1,A2的点P恒满足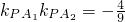 ,则椭圆C的离心率为
,则椭圆C的离心率为
- A.

- B.

- C.

- D.

D
分析:利用斜率公式计算斜率,可得P的轨迹方程,即为椭圆C,从而可求椭圆的离心率.
解答:设P(x,y),则
∴ ,即为P的轨迹方程
,即为P的轨迹方程
∵椭圆C上异于A1,A2的点P恒满足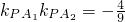 ,
,
∴该方程即为椭圆C
∴椭圆C的离心率为
故选D.
点评:本题考查椭圆的几何性质,考查恒成立问题,属于中档题.
分析:利用斜率公式计算斜率,可得P的轨迹方程,即为椭圆C,从而可求椭圆的离心率.
解答:设P(x,y),则

∴
 ,即为P的轨迹方程
,即为P的轨迹方程∵椭圆C上异于A1,A2的点P恒满足
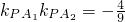 ,
,∴该方程即为椭圆C
∴椭圆C的离心率为

故选D.
点评:本题考查椭圆的几何性质,考查恒成立问题,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,已知A1,A2分别为椭圆
如图,已知A1,A2分别为椭圆 的左右顶点,椭圆C上异于A1,A2的点P恒满足
的左右顶点,椭圆C上异于A1,A2的点P恒满足 ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )



 的下顶点和上顶点,F为椭圆的下焦点,P为椭圆上异于A1,A2点的任意一点,直线A1P,A2P分别交直线l:y=m(m<-2)于M,N点
的下顶点和上顶点,F为椭圆的下焦点,P为椭圆上异于A1,A2点的任意一点,直线A1P,A2P分别交直线l:y=m(m<-2)于M,N点