题目内容
 如图,已知A1,A2分别为椭圆
如图,已知A1,A2分别为椭圆| y2 |
| 4 |
| x2 |
| 3 |
(1)当点P位于y轴右侧,且PF∥l时,求直线A1M的方程;
(2)是否存在m值,使得以MN为直径的圆过F点?若存在加以证明,若不存在,请说明理由;
(3)由(2)问所得m值,求线段MN最小值.
分析:(1)PF∥l时,P点坐标为P(
,-1).由A1(0,-2).能求出直线A1M方程
(2)设A1M:y=k1x-2,由
,得M(
,m),
=(
,m+1).设A2N:y=k2x+2,由
,得N(
,m),
=(
,m+1).若以MN为直径的圆过点F,则
•
=0,由此能求出m=-4.
(3)由m=-4,知M(-
,-4),N(-
,-4),所以|MN|≥2
=6,由此能求出|MN|最小值.
| 3 |
| 2 |
(2)设A1M:y=k1x-2,由
|
| m+2 |
| k1 |
| FM |
| m+2 |
| k1 |
|
| m-2 |
| k2 |
| FN |
| m-2 |
| k2 |
| FM |
| FN |
(3)由m=-4,知M(-
| 2 |
| k1 |
| 6 |
| k2 |
|
解答:解:(1)∵椭圆
+
=1的下焦点F(0,-1),
点P在椭圆上,且点P位于y轴右侧,
∴PF∥l时,P点坐标为P(x,-1),(x>0),
把P(x,-1)(x>0)代入椭圆
+
=1,
得
+
=1,x>0,
解得x=
,∴P(
,-1).
∵A1为椭圆
+
=1的下顶点,
∴A1(0,-2).
∴直线A1M方程:
=
,
即2x-3y-6=0.(3分)
(2)∵A1,A2分别为椭圆
+
=1的下顶点和上顶点,
∴A1(0,-2),A2(0,2),
设A1M:y=k1x-2,由
,得M(
,m),
∴
=(
,m+1).
设A2N:y=k2x+2,由
,得N(
,m),
∴
=(
,m+1).
若以MN为直径的圆过点F,则
•
=0,
得
+(1+m)2=0.(5分)
∵KA1P•KA2P=
•
=
=-
.(7分)
∴
+(m+1)2=0,
∴m=-4.(9分)
(3)∵m=-4,
∴M(-
,-4),N(-
,-4),
∴|MN|=|
-
|=|
-
|=|
+
|=
+
∴|MN|≥2
=6,
当且仅当K2=
,K=±
时,
|MN|最小值为6.(12分)
| y2 |
| 4 |
| x2 |
| 3 |
点P在椭圆上,且点P位于y轴右侧,
∴PF∥l时,P点坐标为P(x,-1),(x>0),
把P(x,-1)(x>0)代入椭圆
| y2 |
| 4 |
| x2 |
| 3 |
得
| 1 |
| 4 |
| x2 |
| 3 |
解得x=
| 3 |
| 2 |
| 3 |
| 2 |
∵A1为椭圆
| y2 |
| 4 |
| x2 |
| 3 |
∴A1(0,-2).
∴直线A1M方程:
| y+2 |
| x |
| -1+2 | ||
|
即2x-3y-6=0.(3分)
(2)∵A1,A2分别为椭圆
| y2 |
| 4 |
| x2 |
| 3 |
∴A1(0,-2),A2(0,2),
设A1M:y=k1x-2,由
|
| m+2 |
| k1 |
∴
| FM |
| m+2 |
| k1 |
设A2N:y=k2x+2,由
|
| m-2 |
| k2 |
∴
| FN |
| m-2 |
| k2 |
若以MN为直径的圆过点F,则
| FM |
| FN |
得
| m2-4 |
| K1K2 |
∵KA1P•KA2P=
| y+2 |
| x-0 |
| y-2 |
| x-0 |
| y2-4 |
| x2 |
| 4 |
| 3 |
∴
| m2-4 | ||
-
|
∴m=-4.(9分)
(3)∵m=-4,
∴M(-
| 2 |
| k1 |
| 6 |
| k2 |
∴|MN|=|
| -2 |
| K1 |
| -6 |
| K2 |
| 2 |
| K1 |
| 6 |
| K2 |
| 2 |
| K1 |
| 9K1 |
| 2 |
| 2 |
| |K1| |
| 9|K1| |
| 2 |
∴|MN|≥2
|
当且仅当K2=
| 4 |
| 9 |
| 2 |
| 3 |
|MN|最小值为6.(12分)
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知曲线
如图,已知曲线
 如图,已知抛物线C:y2=4x,过点P
如图,已知抛物线C:y2=4x,过点P (1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
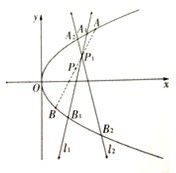
(1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA 的下顶点和上顶点,F为椭圆的下焦点,P为椭圆上异于A1,A2点的任意一点,直线A1P,A2P分别交直线l:y=m(m<-2)于M,N点
的下顶点和上顶点,F为椭圆的下焦点,P为椭圆上异于A1,A2点的任意一点,直线A1P,A2P分别交直线l:y=m(m<-2)于M,N点