题目内容
14.已知$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$,且$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为$\frac{π}{3}$,|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,设$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,则tanθ=( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -1 | D. | -$\frac{\sqrt{3}}{3}$ |
分析 作出图形,将问题转化为解三角形问题.
解答 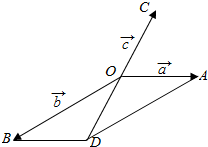 解:如图,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,则∠COA=$\frac{π}{3}$,以OA,OB为邻边作平行四边形OADB,
解:如图,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,则∠COA=$\frac{π}{3}$,以OA,OB为邻边作平行四边形OADB,
则$\overrightarrow{OD}$=$\overrightarrow{a}+\overrightarrow{b}$=-$\overrightarrow{c}$,∠ODB=∠AOD=$\frac{2π}{3}$.BD=OA,OB=$\sqrt{3}$OA.
在△OBD中,由正弦定理得:$\frac{OB}{sin∠ODB}=\frac{BD}{sin∠BOD}$,∴$\frac{\sqrt{3}OA}{\frac{\sqrt{3}}{2}}$=$\frac{OA}{sin∠BOD}$,
解得sin∠BOD=$\frac{1}{2}$,∴∠BOD=$\frac{π}{6}$.∴θ=∠BOD+∠AOD=$\frac{π}{6}+\frac{2π}{3}$=$\frac{5π}{6}$.∴tanθ=-$\frac{\sqrt{3}}{3}$.
故选:D.
点评 本题考查了平面向量加法的几何意义,属于中档题.

练习册系列答案
相关题目
2.已知数列{an}为等差数列,a1+a2+a3=3,a5+a6+a7=9,则a4=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.已知某物体的运动方程是S=t+$\frac{1}{9}$t3,则当t=3s时的瞬时速度是( )
| A. | 10 m/s | B. | 9 m/s | C. | 4 m/s | D. | 3 m/s |
19.(普通中学做)设实数x,y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$,则z=x+y的取值范围是( )
| A. | [4,6] | B. | [0,4] | C. | [2,4] | D. | [2,6] |