题目内容

4．已知函数$f（x）={log_2}（{x^2}-x）$，g（x）=log2（2x-2）．
（1）求f（x）的定义域；
（2）求不等式f（x）＞g（x）的解集．

分析 （1）解不等式x2-x＞0得出f（x）的定义域；
（2）根据对数函数的单调性得出x2-x＞2x-2＞0，解出即可．

解答 解：（1）由f（x）有意义得x2-x＞0，解得x＜0或x＞1，所以f（x）的定义域为{x|x＜0或x＞1}．
（2）∵f（x）＞g（x），即log2（x2-x）＞log2（2x-2），∴x2-x＞2x-2＞0，解得x＞2．
∴不等式的解集为{x|x＞2}．

点评 本题考查了对数函数的定义域，对数函数单调性的应用，属于中档题．

练习册系列答案
相关题目
14．已知$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，且$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为$\frac{π}{3}$，|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|，设$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为θ，则tanθ=（　　）
A．$\sqrt{3}$B．$\frac{\sqrt{3}}{3}$C．-1D．-$\frac{\sqrt{3}}{3}$
15．对于任意的n∈N*，记集合En={1，2，3，…，n}，Pn=$\left\{{x\left|{x=\frac{a}{{\sqrt{b}}}，a∈{E_n}，b∈{E_n}}\right.}\right\}$．若集合A满足下列条件：①A⊆Pn；②?x1，x2∈A，且x1≠x2，不存在k∈N*，使x1+x2=k2，则称A具有性质Ω．
如当n=2时，E2={1，2}，P2=$\{1，2，\frac{1}{{\sqrt{2}}}，\frac{2}{{\sqrt{2}}}\}$．?x1，x2∈P2，且x1≠x2，不存在k∈N*，使x1+x2=k2，所以P2具有性质Ω．
（Ⅰ）写出集合P3，P5中的元素个数，并判断P3是否具有性质Ω．
（Ⅱ）证明：不存在A，B具有性质Ω，且A∩B=∅，使E15=A∪B．
（Ⅲ）若存在A，B具有性质Ω，且A∩B=∅，使Pn=A∪B，求n的最大值．
12．已知定义域为R的函数f（x）=$\frac{{-{2^x}+b}}{{{2^{x+1}}+a}}$（a，b是常数）是奇函数．
（1）求函数f（x）的解析式；
（2）判断函数f（x）的单调性，并证明你的结论；
（3）若对于任意$x∈[{\frac{1}{2}，3}]$都有f（kx2）+f（2x-1）＞0成立，求实数k的取值范围．
19．求值：
$（1）{（-{3^{-\frac{2}{3}}}×{27^{\frac{1}{3}}}）^2}+{log_3}\frac{1}{9}$=$\root{3}{9}-1$；
（2）若|2x-1|+（y-2）2=0，则lg（xy）0．
9．已知正方体ABCD-A1B1C1D1，下列向量的数量积不为0的是（　　）
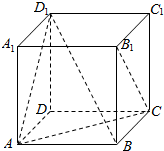
A．$\overrightarrow{A{D}_{1}}•\overrightarrow{{B}_{1}C}$B．$\overrightarrow{B{D}_{1}}•\overrightarrow{AC}$C．$\overrightarrow{B{D}_{1}}•\overrightarrow{BC}$D．$\overrightarrow{AB}•\overrightarrow{A{D}_{1}}$
16．下列不等关系正确的是（　　）
A．log43＜log34B．log${\;}_{\frac{1}{3}}$3＜log${\;}_{\frac{1}{2}}$3
C．3${\;}^{\frac{1}{2}}$$＜{3}^{\frac{1}{3}}$D．3${\;}^{\frac{1}{2}}$＜log32
13．已知α和β均为锐角，且sinα=$\frac{4}{5}$，cosβ=$\frac{12}{13}$．
（1）求sin（α+β）的值；
（2）求tan（α-β）的值．
14．已知关于x的不等式mx2+nx-1＜0的解集为{x|x＜$\frac{1}{3}$，或x＞$\frac{1}{2}$}，则m+n等于-1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网