题目内容
19．（普通中学做）设实数x，y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$，则z=x+y的取值范围是（ ）| A． | [4，6] | B． | [0，4] | C． | [2，4] | D． | [2，6] |
分析 由约束条件作出平面区域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$作出可行域如图，
A（0，2），
联立$\left\{\begin{array}{l}{x-y=2}\\{y=2}\end{array}\right.$，解得B（4，2），
化z=x+y为y=-x+z，
由图可知，当直线y=-x+z过A时，z有最小值，等于2；
当直线y=-x+z过B时，z有最大值，等于6．
故选：D．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
9．两直线3x+4y-5=0与6x+my+15=0（m∈R）平行，则它们之间的距离为（ ）
| A． | 2 | B． | 4 | C． | $\frac{5}{2}$ | D． | 5 |
7．若圆C与圆（x+2）2+（y-1）2=1关于原点对称，则圆C的方程是（ ）
| A． | （x-2）2+（y+1）2=1 | B． | （x-2）2+（y-1）2=1 | C． | （x-1）2+（y+2）2=1 | D． | （x+1）2+（y-2）2=1 |
14．已知$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，且$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为$\frac{π}{3}$，|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|，设$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为θ，则tanθ=（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -1 | D． | -$\frac{\sqrt{3}}{3}$ |
已知函数f（x）=3sin（ωx+φ）（ω＞0，0≤φ＜π）的部分图象如图所示，则该函数的解析式为f（x）=$3sin（\frac{π}{4}x+\frac{π}{4}）$．
9．已知正方体ABCD-A1B1C1D1，下列向量的数量积不为0的是（ ）
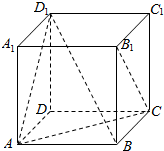
| A． | $\overrightarrow{A{D}_{1}}•\overrightarrow{{B}_{1}C}$ | B． | $\overrightarrow{B{D}_{1}}•\overrightarrow{AC}$ | C． | $\overrightarrow{B{D}_{1}}•\overrightarrow{BC}$ | D． | $\overrightarrow{AB}•\overrightarrow{A{D}_{1}}$ |