题目内容
12.已知函数$f(x)=ax+{log_2}({2^x}+1)$,其中a∈R.(1)当a=-$\frac{1}{2}$时,求证:函数f(x)是偶函数;
(2)已知a>0,函数f(x)的反函数为f-1(x),若函数y=f(x)+f-1(x)在区间[1,2]上的最小值为1+log23,求函数f(x)在区间[1,2]上的最大值.
分析 (1)根据函数奇偶性的定义进行证明即可.
(2)根据f(x)与反函数的单调性相同,根据最小值建立方程关系求出a的值进行求解即可.
解答 解:(1)当a=-$\frac{1}{2}$时,$f(x)=-\frac{1}{2}x+{log_2}({2^x}+1)$,定义域为R,
$f(-x)=\frac{1}{2}x+{log_2}({2^{-x}}+1)$=$\frac{1}{2}x+{log_2}(\frac{{1+{2^x}}}{2^x})$
=$\frac{1}{2}x+{log_2}({2^x}+1)-{log_2}{2^x}$=$-\frac{1}{2}x+{log_2}({2^x}+1)$=f(x),
∴函数f(x)是偶函数.
(2)∵函数f(x)与f-1(x)单调性相同,
∴当a>0时,函数f(x)为增函数,
则y=f(x)+f-1(x)在区间[1,2]上为增函数,
则函数的最小值为当x=1时,y=f(1)+f-1(1)=1+log23,
即a+log23+f-1(1)=1+log23,则f-1(1)=1-a,
即f(1-a)=1,
则a(1-a)+log2(21-a+1)=1,
得a=1,
此时f(x)=x+log2(2x+1)在[1,2]上是增函数,
则函数的最大值为f(2)=2+log2(22+1)=2+log25.
点评 本题主要考查函数奇偶性的判断以及函数单调性的应用,根据函数与反函数的单调性相同建立方程求出a的值是解决本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
3.如图是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{512}$的值的一个程序框图,其中判断框内可以填的是( )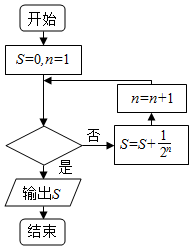

| A. | n≥12? | B. | n≥11? | C. | n≥10? | D. | n≥9? |
17.阅读如图的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为( )


| A. | 21 | B. | 57 | C. | 64 | D. | 73 |
4.执行如图所示的程序框图,输出c的结果为( )
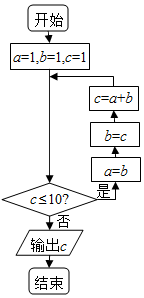

| A. | 13 | B. | 21 | C. | 17 | D. | 15 |
