题目内容
一个几何体的三视图如图所示,则该几何体的体积是 .
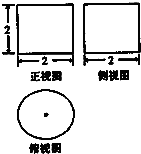

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得,该几何体为圆柱,求出底面面积和高,代入圆柱体积公式,可得答案.
解答:
解:由已知中的三视图可得,该几何体为以俯视图为底面的圆柱,
圆柱的底面面积S=π(
)2=π,
圆柱的高h=2,
故圆柱的体积V=Sh=2π,
故答案为:2π
圆柱的底面面积S=π(
| 2 |
| 2 |
圆柱的高h=2,
故圆柱的体积V=Sh=2π,
故答案为:2π
点评:本题考查三视图、圆柱的体积,本试题考查了简单几何体的三视图的运用.培养同学们的空间想象能力和基本的运算能力.基础题.

练习册系列答案
相关题目
图中的小网格由等大的小正方形拼成,则向量
-
=( )

| a |
| b |

| A、e1+3e2 |
| B、-e1-3e2 |
| C、e1-3e2 |
| D、-e1+3e2 |
某几何体的正视图与侧视频如图所示,则该几何体的俯视图不可能是( )

A、 |
B、 |
C、 |
D、 |
 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,| π |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
设{an}是等差数列,从{a1,a2,a3,…,a20}中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有( )
| A、90个 | B、120个 |
| C、160个 | D、180个 |
若函数f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是( )
| A、(-1,0) |
| B、(0,1] |
| C、(0,1) |
| D、(-1,0)∪(0,1] |