题目内容
椭圆C的中心在原点,焦点在x轴上,两焦点F1,F2之间的距离为2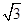 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
(1)求椭圆C的标准方程;
(2)若椭圆C的右顶点为A,直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N,且满足AM⊥AN.求证:直线l过定点,并求出定点的坐标.
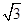 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.(1)求椭圆C的标准方程;
(2)若椭圆C的右顶点为A,直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N,且满足AM⊥AN.求证:直线l过定点,并求出定点的坐标.
(1) +y2=1 (2)见解析
+y2=1 (2)见解析
 +y2=1 (2)见解析
+y2=1 (2)见解析(1)设椭圆的标准方程为 +
+ =1(a>b>0),因为|F1F2|=2
=1(a>b>0),因为|F1F2|=2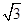 ,所以c=
,所以c=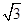 ,由S△PF1F2=1,得|PF1||PF2|=2,又由PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2=12,即(|PF1|+|PF2|)2-2|PF1||PF2|=12,即4a2-4=12,a2=4,b2=a2-3=1,所以椭圆C的标准方程为
,由S△PF1F2=1,得|PF1||PF2|=2,又由PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2=12,即(|PF1|+|PF2|)2-2|PF1||PF2|=12,即4a2-4=12,a2=4,b2=a2-3=1,所以椭圆C的标准方程为 +y2=1.
+y2=1.
(2)由方程组 ,得(1+4k2)x2+8kmx+4m2-4=0,
,得(1+4k2)x2+8kmx+4m2-4=0,
Δ=(8km)2-4(1+4k2)(4m2-4)>0,整理得4k2-m2+1>0.
设M(x1,y1),N(x2,y2),则x1+x2=- ,x1x2=
,x1x2= .
.
由AM⊥AN且椭圆的右顶点为A(2,0),得(x1-2)(x2-2)+y1y2=0,
因为y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
所以(1+k2)x1x2+(km-2)(x1+x2)+m2+4=0,
即(1+k2)· +(km-2)·
+(km-2)· +m2+4=0,
+m2+4=0,
整理得:5m2+16mk+12k2=0,
解得m=-2k或m=- ,均满足4k2-m2+1>0.
,均满足4k2-m2+1>0.
当m=-2k时,直线的l方程为y=kx-2k,过定点(2,0),与题意矛盾,舍去;
当m=- 时,直线l的方程为y=k(x-
时,直线l的方程为y=k(x- ),过定点(
),过定点( ,0),符合题意.
,0),符合题意.
故直线l过定点,且定点的坐标为( ,0).
,0).
 +
+ =1(a>b>0),因为|F1F2|=2
=1(a>b>0),因为|F1F2|=2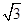 ,所以c=
,所以c=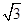 ,由S△PF1F2=1,得|PF1||PF2|=2,又由PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2=12,即(|PF1|+|PF2|)2-2|PF1||PF2|=12,即4a2-4=12,a2=4,b2=a2-3=1,所以椭圆C的标准方程为
,由S△PF1F2=1,得|PF1||PF2|=2,又由PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2=12,即(|PF1|+|PF2|)2-2|PF1||PF2|=12,即4a2-4=12,a2=4,b2=a2-3=1,所以椭圆C的标准方程为 +y2=1.
+y2=1.(2)由方程组
 ,得(1+4k2)x2+8kmx+4m2-4=0,
,得(1+4k2)x2+8kmx+4m2-4=0,Δ=(8km)2-4(1+4k2)(4m2-4)>0,整理得4k2-m2+1>0.
设M(x1,y1),N(x2,y2),则x1+x2=-
 ,x1x2=
,x1x2= .
.由AM⊥AN且椭圆的右顶点为A(2,0),得(x1-2)(x2-2)+y1y2=0,
因为y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
所以(1+k2)x1x2+(km-2)(x1+x2)+m2+4=0,
即(1+k2)·
 +(km-2)·
+(km-2)· +m2+4=0,
+m2+4=0,整理得:5m2+16mk+12k2=0,
解得m=-2k或m=-
 ,均满足4k2-m2+1>0.
,均满足4k2-m2+1>0.当m=-2k时,直线的l方程为y=kx-2k,过定点(2,0),与题意矛盾,舍去;
当m=-
 时,直线l的方程为y=k(x-
时,直线l的方程为y=k(x- ),过定点(
),过定点( ,0),符合题意.
,0),符合题意.故直线l过定点,且定点的坐标为(
 ,0).
,0).
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

 ,0)和F2(
,0)和F2( ·
·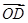 =0(O为坐标原点),求直线l的方程.
=0(O为坐标原点),求直线l的方程.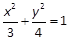 的左右两个顶点, P是该椭圆上异于A,B的任一点,则
的左右两个顶点, P是该椭圆上异于A,B的任一点,则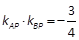 .
.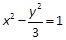 的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则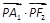 的最小值为-2.
的最小值为-2.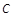 :
: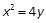 的焦点为
的焦点为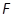 ,抛物线上一点
,抛物线上一点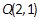 和抛物线内一点
和抛物线内一点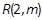
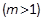 ,过点Q作抛物线的切线
,过点Q作抛物线的切线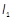 ,直线
,直线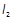 过点
过点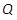 且与
且与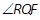 ;
;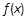 是定义在R上的奇函数,
是定义在R上的奇函数,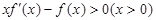 , 则不等式
, 则不等式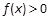 的解集是
的解集是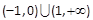 .
. +
+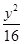 =1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( ) +
+ =1(a>b>0)的左、右焦点,点P(-
=1(a>b>0)的左、右焦点,点P(- ,1)在椭圆上,线段PF2与y轴的交点M满足
,1)在椭圆上,线段PF2与y轴的交点M满足 +
+ =0.
=0. 的离心率
的离心率 ,
, 分别为椭圆的长轴和短轴的端点,
分别为椭圆的长轴和短轴的端点, 为
为 中点,
中点, 为坐标原点,且
为坐标原点,且 .
. 的直线
的直线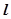 交椭圆于
交椭圆于 两点,求
两点,求 面积最大时,直线
面积最大时,直线 +
+ =1(m<6)与曲线
=1(m<6)与曲线 +
+ =1(5<n<9)的( )
=1(5<n<9)的( )