题目内容
11.下面四组函数中,函数f(x)和g(x)表示同一函数的是( )| A. | f(x)=$\sqrt{x-1}$•$\sqrt{x+3}$,g(x)=$\sqrt{{x}^{2}+2x-3}$ | B. | f(x)=$\frac{{x}^{2}-2x+1}{x-1}$,g(x)=x-1 | ||
| C. | f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|}$,g(x)=$\frac{\sqrt{1-{x}^{2}}}{x+2}$ | D. | 以上三组都不是同一函数 |
分析 根据两个函数是同一个函数的定义,判断它们的定义域相同,对应关系(解析式)也相同,即可判断它们是相同函数.
解答 解:对于A,f(x)=$\sqrt{x-1}$•$\sqrt{x+3}$=$\sqrt{(x-1)(x+3)}$(x≥1),与g(x)=$\sqrt{{x}^{2}+2x-3}$=$\sqrt{(x-1)(x+3)}$(x≤-3或x≥1)的定义域不同,所以不是同一函数;
对于B,f(x)=$\frac{{x}^{2}-2x+1}{x-1}$=x-1(x≠1)与g(x)=x-1(x∈R)的定义域不同,所以不是同一函数;
对于C,f(x)=$\frac{\sqrt{1{-x}^{2}}}{|x+2|}$=$\frac{\sqrt{1{-x}^{2}}}{x+2}$(-1≤x≤1)与g(x)=$\frac{\sqrt{1{-x}^{2}}}{x+2}$(-1≤x≤1)的定义域相同,对应关系也相同,所以是同一函数.
故选:C.
点评 本题考查了判断两个函数是否为同一函数的应用问题,解题时应判断两个函数的定义域是否相同,对应关系是否也相同,是基础题目.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
1.已知△ABC中,bcosB=ccosC,则△ABC的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰或直角三角形 | D. | 等边三角形 |
3.如图,已知AB⊥平面BCD,BC⊥CD,M是CD的中点.则二面角A-CD-B的平面角是( )
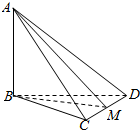

| A. | ∠ADB | B. | ∠BDC | C. | ∠AMB | D. | ∠ACB |
1.为了考察高中生的性别与是否喜欢数学课程之间的关系,在我市的某校高中生中随即抽取了100名学生,得到如下联表:
由表中数据,计算得K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$≈3.03,
附表:
参照附表,则下列结论正确的是( )
| 不喜欢数学课程 | 喜欢数学课程 | 总计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 总 | 75 | 25 | 100 |
附表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
| A. | 有90%以上的把握认为“性别与是否喜欢数学课程有关” | |
| B. | 有90%以上的把握认为“性别与是否喜欢数学课程没有关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程没有关” |
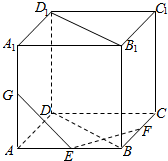 如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,
如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,