题目内容

14．设命题p：有的三角形是等边三角形；命题q：每一个四边形的四顶点共圆．则下列复合命题是真命题的是（　　）
A．p∧￢qB．￢p∧qC．p∧qD．￢p∨q

分析 先判定命题p与q的真假，再利用复合命题真假的判定方法即可得出．

解答 解：命题p：有的三角形是等边三角形，是真命题；
命题q：每一个四边形的四顶点共圆，是假命题．
则下列复合命题是真命题的只有p∧￢q．
故选：A．

点评 本题考查了特称命题的判定方法、复合命题真假的判定方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
4．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的长轴长为$2\sqrt{2}$，离心率$e=\frac{{\sqrt{2}}}{2}$，过右焦点F的直线l交椭圆于P，Q两点．
（Ⅰ）求椭圆的方程；
（Ⅱ）当直线l的斜率为1时，求△POQ的面积；
（Ⅲ）若以OP，OQ为邻边的平行四边形是矩形，求满足该条件的直线l的方程．
5．椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的左、右焦点分别为F1、F2，则椭圆上满足PF1⊥PF2的点P（　　）
A．有2个B．有4个C．不一定存在D．一定不存在
2．已知椭圆C：$\frac{x^2}{8}+\frac{y^2}{n}=1$的离心率为$\frac{{\sqrt{2}}}{2}$，F是椭圆C的右焦点．过点F且斜率为k（k≠0）的直线l与椭圆C交于A，B两点，O是坐标原点．
（Ⅰ）求n的值；
（Ⅱ）若线段AB的垂直平分线在y轴的截距为$\frac{2}{3}$，求k的值；
（Ⅲ）是否存在点P（t，0），使得PF为∠APB的平分线？若存在，求出t的值；若不存在，说明理由．
9．若直线l的方向向量为$\overrightarrow{a}$=（1，0，2），平面α的法向量为$\overrightarrow{n}$=（-2，0，-4），则（　　）
A．l∥αB．l⊥α
C．l?αD．l与α相交但不垂直
19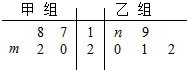．某车间将10名工人评价分成甲、乙两组加工某种零件，在单位时间内每个工人加工的合格零件数如茎叶图所示．已知两组工人在单位时间内加工的合格零件平均数都为20，则有（　　）
A．m=3，n=8B．m=4，n=7C．m=5，n=6D．m=6，n=5
6．已知直线l：2x-y+m=0，m∈R，圆C：x2+y2=5．
（Ⅰ）当m为何值时，l与C无公共点；
（Ⅱ）当m为何值时，l被C截得的弦长为2．
3．椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1的左、右焦点分别为F1，F2，弦AB过点F1，若△ABF2的内切圆周长为π，A，B两点的坐标分别为（x1，y1），（x2，y2），则|y1-y2|=$\frac{4}{3}$．
4．在△ABC中，若$A=\frac{π}{6}，a=2，b=2\sqrt{3}$，则B=（　　）
A．$\frac{π}{6}$或$\frac{5π}{6}$B．$\frac{π}{3}$C．$\frac{π}{3}$或$\frac{2π}{3}$D．$\frac{2π}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网