题目内容
2.已知椭圆C:$\frac{x^2}{8}+\frac{y^2}{n}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是椭圆C的右焦点.过点F且斜率为k(k≠0)的直线l与椭圆C交于A,B两点,O是坐标原点.(Ⅰ)求n的值;
(Ⅱ)若线段AB的垂直平分线在y轴的截距为$\frac{2}{3}$,求k的值;
(Ⅲ)是否存在点P(t,0),使得PF为∠APB的平分线?若存在,求出t的值;若不存在,说明理由.
分析 (Ⅰ)运用离心率公式和a,b,c的关系,可得n=4;
(Ⅱ)求得椭圆方程,设出直线AB的方程,代入椭圆方程,运用韦达定理和中点坐标公式,再由两直线垂直的条件:斜率之积为-1,计算即可得到所求值;
(Ⅲ)假设存在点P(t,0),使得PF为∠APB的平分线,即有直线PA和PB的斜率之和为0,运用韦达定理和斜率公式,化简整理,解方程可得t,即可判断存在.
解答 解:(Ⅰ)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a=2$\sqrt{2}$,
即有c=2,b=2,
即有n=4;
(Ⅱ)椭圆的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1,F(2,0),
直线AB的方程为y=k(x-2),代入椭圆方程可得
(1+2k2)x2-8k2x+8k2-8=0,
x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{8{k}^{2}-8}{1+2{k}^{2}}$,
AB的中点为($\frac{4{k}^{2}}{1+2{k}^{2}}$,k($\frac{4{k}^{2}}{1+2{k}^{2}}$-2)),
即为($\frac{4{k}^{2}}{1+2{k}^{2}}$,$\frac{-2k}{1+2{k}^{2}}$),
由题意可得$\frac{\frac{-2k}{1+2{k}^{2}}-\frac{2}{3}}{\frac{4{k}^{2}}{1+2{k}^{2}}}$=-$\frac{1}{k}$,解得k=1或$\frac{1}{2}$;
(Ⅲ)假设存在点P(t,0),使得PF为∠APB的平分线,
即有直线PA和PB的斜率之和为0,
即有$\frac{{y}_{1}}{{x}_{1}-t}$+$\frac{{y}_{2}}{{x}_{2}-t}$=0,由y1=k(x1-2),y2=k(x2-2),
即有2x1x2-(2+t)(x1+x2)+4t=0,
代入韦达定理,可得$\frac{16{k}^{2}-16}{1+2{k}^{2}}$-(2+t)•$\frac{8{k}^{2}}{1+2{k}^{2}}$+4t=0,
化简可得t=4.
即有存在点P(4,0),使得PF为∠APB的平分线.
点评 本题考查椭圆的方程的求法,考查直线方程和椭圆方程联立,运用韦达定理和中点坐标公式,同时考查直线的斜率公式的运用,考查化简整理的运算能力,属于中档题.

| A. | $[-2,\sqrt{3}]$ | B. | $[-\frac{{\sqrt{3}}}{2},1]$ | C. | $[-\sqrt{3},\sqrt{3}]$ | D. | $[-\frac{{\sqrt{3}}}{2},\sqrt{3}]$ |
| A. | x-y+1=0,2x-y=0 | B. | x-y-1=0,x-2y=0 | C. | x+y+1=0,2x+y=0 | D. | x-y+1=0,x+2y=0 |
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
| A. | p∧¬q | B. | ¬p∧q | C. | p∧q | D. | ¬p∨q |
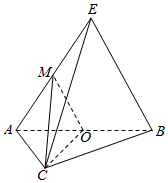 如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.
如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.