题目内容
6.已知直线l:2x-y+m=0,m∈R,圆C:x2+y2=5.(Ⅰ)当m为何值时,l与C无公共点;
(Ⅱ)当m为何值时,l被C截得的弦长为2.
分析 (Ⅰ)根直线和圆的位置关系进行求解即可;
(Ⅱ)根据直线和圆相交时的弦长公式进行求解即可.
解答 解:(Ⅰ)由已知,圆心为O(0,0),半径r=$\sqrt{5}$,
圆心到直线2x-y+m=0的距离d=$\frac{|m|}{{\sqrt{{2^2}+{{(-1)}^2}}}}$=$\frac{|m|}{\sqrt{5}}$,…(2分)
∵直线与圆无公共点,∴d>r,即$\frac{|m|}{\sqrt{5}}$>$\sqrt{5}$,…(4分)
∴m>5或m<-5.
故当m>5或m<-5时,直线与圆无公共点.…(5分)
(Ⅱ)如图,由平面几何垂径定理知r2-d2=12.…(7分)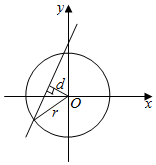
即5-$\frac{m2}{5}$=1,得m=±2$\sqrt{5}$,
∴当m=±2$\sqrt{5}$时,直线被圆截得的弦长为2.…(10分)
点评 本题主要考查直线和圆的位置关系的判断和应用,根据直线和圆相交时的弦长公式是解决本题的关键.

练习册系列答案
相关题目
16.高一年级某同学用“五点法”画函数$y=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象时,列表并填入部分数据,如表:
(1)请将上面表格中的数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)求函数f(x)的单调递增区间.
| x | $\frac{π}{4}$ | $\frac{3π}{4}$ | $\frac{5π}{4}$ | ||
| ωx+φ | 0 | $\frac{π}{2}$ | $\frac{3π}{2}$ | 2π | |
| f(x) | 0 | 2 | -2 | 0 |
(2)求函数f(x)的单调递增区间.
17.函数$f(x)={log_{\frac{1}{2}}}({{x^2}-4})$的单调递增区间为( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
14.设命题p:有的三角形是等边三角形;命题q:每一个四边形的四顶点共圆.则下列复合命题是真命题的是( )
| A. | p∧¬q | B. | ¬p∧q | C. | p∧q | D. | ¬p∨q |
1.下列说法正确的是( )
| A. | $?x∈{R}\;,\;\root{3}{x}+1>0$ | |
| B. | 在线性回归分析中,如果两个变量的相关性越强,则相关系数r就越接近于1 | |
| C. | p∨q为真命题,则命题p和q均为真命题 | |
| D. | 命题“$?{x_0}∈{R}\;,\;x_0^2-{x_0}>0$”的否定是“?x∈R,x2-x≤0” |
18.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{1}{3}+2π$ | B. | $\frac{{11+\sqrt{2}}}{2}π+1$ | C. | $\frac{{11π+\sqrt{2}}}{2}$ | D. | $\frac{11π}{2}+\sqrt{2}π$ |
15.将函数$f(x)=1+cos2x-2{sin^2}(x-\frac{π}{6})$的图象右移$\frac{π}{6}$个单位后,所得函数的下列结论中正确的是( )
| A. | 是最小正周期为2π的偶函数 | B. | 是最小正周期为2π的奇函数 | ||
| C. | 是最小正周期为π的偶函数 | D. | 是最小正周期为π的奇函数 |