题目内容
5.椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的左、右焦点分别为F1、F2,则椭圆上满足PF1⊥PF2的点P( )| A. | 有2个 | B. | 有4个 | C. | 不一定存在 | D. | 一定不存在 |
分析 由椭圆方程求出椭圆的焦距与短半轴长,由此可得以F1F2为直径的圆与椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1无交点,则答案可求.
解答 解:由椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1,得a2=25,b2=16,
∴c2=a2-b2=9,则c=3,
∴F1(-3,0),F2(3,0),
∵b=4>3=c,
∴以F1F2为直径的圆与椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1无交点,
则椭圆上满足PF1⊥PF2的点P一定不存在.
故选:D.
点评 本题考查椭圆的简单性质,考查了数学转化思想方法,是基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15.不等式x2-x>0的解集是( )
| A. | (1,+∞) | B. | (0,1) | C. | (-∞,0) | D. | (-∞,0)∪(1,+∞) |
16.高一年级某同学用“五点法”画函数$y=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象时,列表并填入部分数据,如表:
(1)请将上面表格中的数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)求函数f(x)的单调递增区间.
| x | $\frac{π}{4}$ | $\frac{3π}{4}$ | $\frac{5π}{4}$ | ||
| ωx+φ | 0 | $\frac{π}{2}$ | $\frac{3π}{2}$ | 2π | |
| f(x) | 0 | 2 | -2 | 0 |
(2)求函数f(x)的单调递增区间.
13.直线l将圆x2+y2-2x+4y=0平分,且在两坐标轴上的截距相等,则直线l的方程是( )
| A. | x-y+1=0,2x-y=0 | B. | x-y-1=0,x-2y=0 | C. | x+y+1=0,2x+y=0 | D. | x-y+1=0,x+2y=0 |
17.函数$f(x)={log_{\frac{1}{2}}}({{x^2}-4})$的单调递增区间为( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
14.设命题p:有的三角形是等边三角形;命题q:每一个四边形的四顶点共圆.则下列复合命题是真命题的是( )
| A. | p∧¬q | B. | ¬p∧q | C. | p∧q | D. | ¬p∨q |
15.将函数$f(x)=1+cos2x-2{sin^2}(x-\frac{π}{6})$的图象右移$\frac{π}{6}$个单位后,所得函数的下列结论中正确的是( )
| A. | 是最小正周期为2π的偶函数 | B. | 是最小正周期为2π的奇函数 | ||
| C. | 是最小正周期为π的偶函数 | D. | 是最小正周期为π的奇函数 |
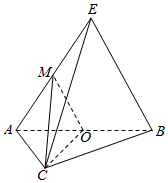 如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.
如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.