题目内容
14.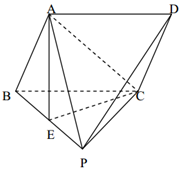 如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.
如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.(Ⅰ)求证:PD∥平面ACE
(Ⅱ)若AB⊥PA,BC=2,求点P到平面ABCD的距离.
分析 (Ⅰ)连结BD交AC于点F,推导出PD∥EF,由此能证明PD∥平面ACE.
(Ⅱ)推导出AE⊥平面PBC,AB⊥PA,设点P到平面ABCD的距离为d,由VP-ABC=VA-PBC,能求出点P到平面ABCD的距离.
解答 证明:(Ⅰ)连结BD交AC于点F.
∵四边形ABCD是平行四边形,∴F是BD的中点,
又E是PB的中点,∴PD∥EF,
又PD?平面ACE,EF?平面ACE,
∴PD∥平面ACE.
解:(Ⅱ)∵点A在平面PBC的正投影恰好是PB的中点,
∴AE⊥平面PBC,E是PB的中点,
又CE,PB?平面PBC,∴AE⊥CE,AE⊥PB.
在△PAB中,E是PB的中点,AB⊥PA,
∴△PAB是等腰直角三角形,AE=1,AB=$\sqrt{2}$,
在等边△PBC中,CE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
在Rt△ACE中,AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=2,
在等腰△ABC中,${S}_{△ABC}=\frac{1}{2}×\sqrt{2}×\sqrt{{2}^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{7}}{2}$.
设点P到平面ABCD的距离为d,
由VP-ABC=VA-PBC,得$\frac{1}{3}{S}_{△ABC}•d=\frac{1}{3}{S}_{△PBC}•AE$,
∴点P到平面ABCD的距离d=$\frac{AE•{S}_{△PBC}}{{S}_{△ABC}}$=$\frac{2\sqrt{3}}{\sqrt{7}}$=$\frac{2\sqrt{21}}{7}$.
点评 本题考查线面平行的证明,考查点到平面的距离的求法,考查推理论证能力、运算求解能力、空间思维能力,考查化归转化思想、数形结合思想,是中档题.

| A. | 0<m<1 | B. | -4<m<0 | C. | m<1 | D. | -3<m<1 |
| A. | 1 | B. | 5 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\sqrt{5}$ |
 如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)
如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)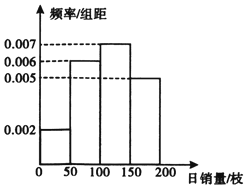 某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.
某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.