题目内容
2.在平面直角坐标系上,有一点列${P_1},{P_2},…,{P_{n-1}},{P_n},…({n∈{N^*}})$,设点Pn的坐标(n,an),其中${a_n}=\frac{2}{n}(n∈{N^*})$,过点Pn,Pn+1的直线与两坐标轴所围成的三角形面积为bn,设Sn表示数列{bn}的前n项和,则S5=$\frac{125}{6}$.分析 先根据题意求出过点Pn,Pn+1的直线方程为y-$\frac{2}{n}$=-$\frac{2}{n(n+1)}$(x-n),分别令x=0,y=0,表示出bn=4+$\frac{1}{n}$-$\frac{1}{n+1}$,再分组求和即可.
解答 解:由题意可得Pn的坐标(n,$\frac{2}{n}$),Pn+1的坐标为(n+1,$\frac{2}{n+1}$),
则过点Pn,Pn+1的直线方程为y-$\frac{2}{n}$=-$\frac{2}{n(n+1)}$(x-n),
令x=0,解得y=$\frac{2}{n}$+$\frac{2}{n+1}$,
令y=0,解得x=2n+1,
∴bn=$\frac{1}{2}$•($\frac{2}{n}$+$\frac{2}{n+1}$)(2n+1)=2+$\frac{n+1}{n}$+$\frac{n}{n+1}$=4+$\frac{1}{n}$-$\frac{1}{n+1}$
∴Sn=4n+1-$\frac{1}{2}$+$\frac{1}{2}$$-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=4n+1-$\frac{1}{n+1}$=4n+$\frac{n}{n+1}$,
∴S5=20+$\frac{5}{6}$=$\frac{125}{6}$,
故答案为:$\frac{125}{6}$
点评 本题考查了数列在解析几何中的应用,以及直线方程的求法和三角形的面积公式,考查了学生的分析问题,解决问题的能力,属于中档题

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.若角α的终边经过点P0(-3,-4),则tanα=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
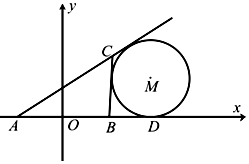 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.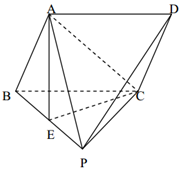 如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.
如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.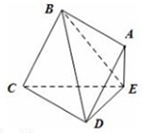 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.