题目内容
6.已知函数$f(x)=a{x^{\frac{3}{2}}}-lnx-\frac{2}{3}$的图象的一条切线为x轴.(Ⅰ)求实数a的值;
(Ⅱ)令g(x)=|f(x)+f'(x)|,若不相等的两个实数x1,x2满足g(x1)=g(x2),求证:x1x2<1.
分析 (Ⅰ)设出切点坐标,得到关于a的方程组,求出a的值即可;
(Ⅱ)令$h(x)=\frac{2}{3}({x^{\frac{3}{2}}}-1)+\sqrt{x}-\frac{1}{x}-lnx$,根据函数的单调性求出g(x)的表达式,令G(x)=g(x)-g($\frac{1}{x}$),根据函数的单调性得到$g(x)-g(\frac{1}{x})>0$,从而证明结论即可.
解答 解:(Ⅰ)$f'(x)=\frac{3a}{2}\sqrt{x}-\frac{1}{x}$,x>0,
设切点坐标为(x0,0),
由题意得$\left\{\begin{array}{l}f({x_0})=a{x_0}^{\frac{3}{2}}-ln{x_0}-\frac{2}{3}=0\\ f'({x_0})=\frac{3a}{2}\sqrt{x_0}-\frac{1}{x_0}=0\end{array}\right.$,解得$\left\{\begin{array}{l}{x_0}=1\\ a=\frac{2}{3}.\end{array}\right.$;
(Ⅱ)证明:$g(x)=|\frac{2}{3}({x^{\frac{3}{2}}}-1)+\sqrt{x}-\frac{1}{x}-lnx|$,令$h(x)=\frac{2}{3}({x^{\frac{3}{2}}}-1)+\sqrt{x}-\frac{1}{x}-lnx$,
则$h'(x)=(\sqrt{x}-\frac{1}{x})+(\frac{1}{{2\sqrt{x}}}+\frac{1}{x^2})$,当x≥1时,$\sqrt{x}-\frac{1}{x}≥0$,h'(x)>0,
h'(x)又可以写成$(\sqrt{x}+\frac{1}{{2\sqrt{x}}})+\frac{1-x}{x^2}$,当0<x<1时,$\frac{1-x}{x^2}>0$,h'(x)>0.
因此h'(x)在(0,+∞)上大于0,h(x)在(0,+∞)上单调递增,又h(1)=0,
因此h(x)在(0,1)上小于0,在(1,+∞)上大于0,
$g(x)=\left\{\begin{array}{l}h(x),x≥1\\-h(x),0<x<1\end{array}\right.$且g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,g(1)=0.
当x>1时,$0<\frac{1}{x}<1$,
记$G(x)=g(x)-g(\frac{1}{x})=h(x)-[{-h(\frac{1}{x})}]=f(x)+f'(x)+f(\frac{1}{x})+f'(\frac{1}{x})$,
记函数y=f'(x)的导函数为y=f''(x),
则$G'(x)=f'(x)+f''(x)-\frac{1}{x^2}f'(\frac{1}{x})-\frac{1}{x^2}f''(\frac{1}{x})$
=$(\sqrt{x}-\frac{1}{x})+(\frac{1}{{2\sqrt{x}}}+\frac{1}{x^2})-\frac{1}{x^2}(\frac{1}{{\sqrt{x}}}-x)-\frac{1}{x^2}(\frac{{\sqrt{x}}}{2}+{x^2})$
=$(\sqrt{x}-1)+\frac{x-1}{{2x\sqrt{x}}}+\frac{{\sqrt{x}-1}}{{{x^2}\sqrt{x}}}>0$,
故G(x)在(1,+∞)上单调递增,
所以G(x)>G(1)=0,所以$g(x)-g(\frac{1}{x})>0$,
不妨设0<x1<1<x2,则$g({x_1})=g({x_2})>g(\frac{1}{x_2})$,
而0<x1<1,$0<\frac{1}{x_2}<1$,有单调性知${x_1}<\frac{1}{x_2}$,即x1x2<1.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及转化思想,是一道综合题.

| A. | 有一个对称中心$({\frac{π}{12},0})$ | B. | 有一条对称轴$x=\frac{π}{6}$ | ||
| C. | 在区间$[{-\frac{π}{12},\frac{5π}{12}}]$上单调递减 | D. | 在区间$[{-\frac{5π}{12},\frac{π}{12}}]$上单调递增 |
①若a∥b,则a∥c,b∥c;
②若a∩b=O,则O∈c;
③若a⊥b,b⊥c,则a⊥c.
其中正确的命题是( )
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①② |
| A. | 25 | B. | 49 | C. | -15 | D. | 40 |
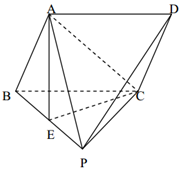 如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.
如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.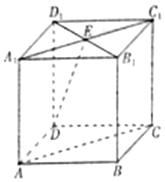 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.