题目内容
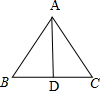
已知锐角△ABC中,角A,B,C的对边分别为a,b,c,外接圆半径为1,D为边BC上一点,
•
=0,向量
=(sinA,a),
=(sinB,c),且
∥
,则AD+BC的取值范围为( )
| AD |
| BC |
| m |
| n |
| m |
| n |
A、(0,
| ||
B、(2,
| ||
C、(3,
| ||
| D、(2,3) |
考点:平面向量数量积的运算,平行向量与共线向量
专题:计算题
分析:由已知,得出△ABC为等腰三角形,AD⊥BD,利用正弦定理得出AD+BC=f(A)=2sinA+1+cosA=1+
sin(A+θ),再利用三角函数性质求范围即可.
| 5 |
解答:
 解:∵
解:∵
•
=0,∴AD⊥BD,
∵向量
=(sinA,a),
=(sinB,c),且
∥
,
∴csinA=asinB,ca=cb,b=c,锐角△ABC为等腰三角形.
根据正弦定理得出BC=2RsinA=2sinA,
在RT△ABD中,AD=tanB×BD=cot
×
BC=
×2sinA=1+cosA,
所以AD+BC=2sinA+1+cosA=1+
sin(A+θ),
其中tanθ=
,θ为锐角(即θ=arctan
),A∈(0,
).
当sin(A+θ)=1时,取得最大值
+1,当A→0时,sin(A+θ)→sinθ=
,此时AD+BC→2.
综上所述AD+BC的取值范围(2,
+1]
故选:B.
 解:∵
解:∵| AD |
| BC |
∵向量
| m |
| n |
| m |
| n |
∴csinA=asinB,ca=cb,b=c,锐角△ABC为等腰三角形.
根据正弦定理得出BC=2RsinA=2sinA,
在RT△ABD中,AD=tanB×BD=cot
| A |
| 2 |
| 1 |
| 2 |
| 1+cosA |
| sinA |
所以AD+BC=2sinA+1+cosA=1+
| 5 |
其中tanθ=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
当sin(A+θ)=1时,取得最大值
| 5 |
| ||
| 5 |
综上所述AD+BC的取值范围(2,
| 5 |
故选:B.
点评:本题考查三角知识的综合应用,建立AD+BC=f(A)=2sinA+1+cosA是关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
函数f(x)=
的定义域为( )
| (x+2)2 | ||
|
| A、{x|x>0} |
| B、{x|x<0} |
| C、{x|x>0,x≠1} |
| D、{x|x<0.x≠-2} |
已知命题p:?x∈R,x2+x+1>0,命题q:?x∈Q,x2=3,则下列命题中是真命题的是( )
| A、p∧q | B、¬p∨q |
| C、¬p∧¬q | D、¬p∨¬q |
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则四面体A-EFB的体积为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则四面体A-EFB的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果数列{an}满足a1=-60,an+1=an+3,那么S10=( )
| A、-180 | B、-465 |
| C、-600 | D、735 |
已知x>0,若x+
的值最小,则x为( )
| 81 |
| x |
| A、81 | B、9 | C、3 | D、16 |
对于命题“正三角形内任意一点到各边的距离之和为定值”推广到空间是“正四面体内任意一点到各面的距离之和为( )”
| A、定值 |
| B、有时为定值,有时为变数 |
| C、变数 |
| D、与正四面体无关的常数 |