题目内容
某市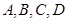 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 | 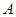 |  | 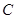 | 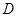 |
| 人数 | 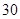 | 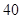 | 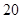 | 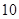 |
(1)问
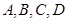 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?(2)从参加问卷调查的
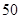 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;(3)在参加问卷调查的
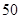 名学生中,从自
名学生中,从自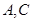 两所中学的学生当中随机抽取两名学
两所中学的学生当中随机抽取两名学生,用
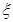 表示抽得
表示抽得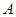 中学的学生人数,求
中学的学生人数,求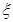 的分布列和期望.
的分布列和期望.
(1) 从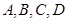 四所中学抽取的学生人数分别为
四所中学抽取的学生人数分别为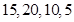 ;(2) 这两名学生自同一所中学的概率为
;(2) 这两名学生自同一所中学的概率为 ,(3)
,(3)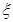 的分布列为:
的分布列为: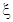

1 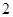
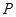

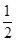
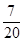
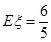 .
.
解析试题分析:(1) 由题意知,四所中学报名参加该高校今年自主招生的学生总人数为100名,抽取的样本容量与总体个数的比值为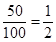 .据此即可计算出答案;(2) 利用组合的意义分别计算出从参加问卷调查的50名学生中随机抽取两名学生的方法和这两名学生来自同一所中学的取法,再利用古典概型的概率计算公式即可得出;(3)由(1) 知,在参加问卷调查的50名学生中,来自A,C两所中学的学生人数分别为15,10.可得ξ的可能取值为0,1,2.利用超几何分布的概率计算公式
.据此即可计算出答案;(2) 利用组合的意义分别计算出从参加问卷调查的50名学生中随机抽取两名学生的方法和这两名学生来自同一所中学的取法,再利用古典概型的概率计算公式即可得出;(3)由(1) 知,在参加问卷调查的50名学生中,来自A,C两所中学的学生人数分别为15,10.可得ξ的可能取值为0,1,2.利用超几何分布的概率计算公式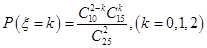 ,即可得到分布列,利用数学期望的概率计算公式即可得出.
,即可得到分布列,利用数学期望的概率计算公式即可得出.
试题解析:(1) 由题意知,四所中学报名参加该高校今年自主招生的学生总人数为100名,
抽取的样本容量与总体个数的比值为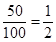 .
.
∴应从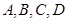 四所中学抽取的学生人数分别为
四所中学抽取的学生人数分别为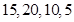 . 4分
. 4分
(2) (2) 设“从参加问卷调查的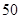 名学生中随机抽取两名学生,求这两名学生自同一所中学”为事件
名学生中随机抽取两名学生,求这两名学生自同一所中学”为事件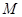 ,从参加问卷调查的
,从参加问卷调查的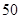 名学生中随机抽取两名学生随机抽取两名学生的取法有
名学生中随机抽取两名学生随机抽取两名学生的取法有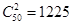 种,这两名学生来自同一所中学的取法有
种,这两名学生来自同一所中学的取法有 ,所以
,所以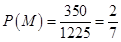 .从参加问卷调查的
.从参加问卷调查的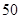 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率 ; 7分
; 7分
(3)由(1)知,在参加问卷调查的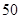 名学生中,自
名学生中,自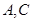 两所中学的学生人数分别
两所中学的学生人数分别
为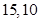 .
.
依题意得,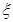 的可能取值为
的可能取值为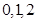 , 8分
, 8分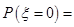

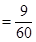 ,
, 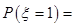

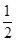 ,
,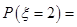
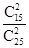
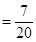 . 11分
. 11分
∴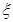 的分布列为:
的分布列为: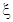

1 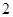
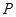

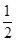
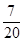
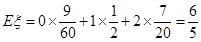 12分
12分
考点:离散型随机变量及其分布列;等可能事件的概率.

某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 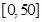 | 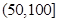 | 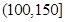 | 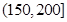 | 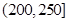 | 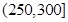 | 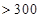 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
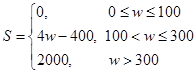 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面
 列联表,并判断能否有
列联表,并判断能否有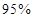 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
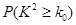 | 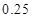 | 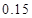 | 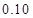 | 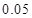 | 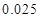 | 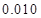 | 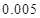 | 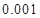 |
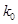 | 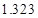 | 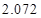 | 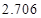 | 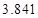 | 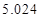 | 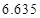 | 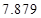 | 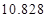 |
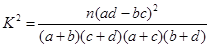
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出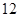 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 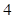 | 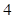 | 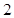 | 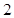 |
(Ⅰ)求这两名队员来自同一学校的概率;
(Ⅱ)设选出的两名队员中来自学校甲的人数为
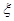 ,求随机变量
,求随机变量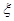 的分布列及数学期望
的分布列及数学期望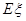 .
. 学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望. 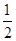 .
.
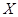 ,求随机变量
,求随机变量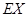 .
.
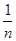 [(x1-
[(x1- )2+(x2-
)2+(x2-