题目内容
12．已知复数z足zi=-1+i，则z等于（ ）| A． | -1-i | B． | 1-i | C． | -1+i | D． | 1+i |
分析 利用复数的运算法则即可得出．
解答 解：∵zi=-1+i，
∴-i•zi=-i（-1+i），
∴z=i+1，
故选：D．
点评 本题考查了复数的运算法则，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}+3x，x＜0\\ ln（x+1），x≥0\end{array}\right.$，若|f（x）|≥ax，则a的取值范围是（ ）
| A． | （-∞，0] | B． | （-∞，1] | C． | [-3，0] | D． | [-3，1] |
3．执行如图所示的程序框图，则输出的S为（ ）
| A． | 2 | B． | $\frac{1}{3}$ | C． | -$\frac{1}{2}$ | D． | -3 |
20．函数$f（x）=3sin（2x-\frac{π}{3}+ϕ），ϕ∈（0，π）$满足f（|x|）=f（x），则ϕ的值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
17．执行如图所示程序图，若N=7时，则输出的结果S的值为（ ）
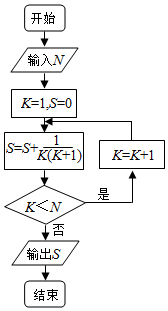
| A． | $\frac{8}{7}$ | B． | $\frac{6}{5}$ | C． | $\frac{7}{8}$ | D． | $\frac{5}{6}$ |
1．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F，若点F关于双曲线的渐近线的对称点在双曲线的右支上，则该双曲线的离心率是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
2．已知点F（-c，0）（c＞0）是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左焦点，过F作直线与圆x2+y2=a2相切，并与渐近线交于第一象限内一点P，满足|$\overrightarrow{OF}$|=|$\overrightarrow{OP}$|，则该双曲线的离心率等于（ ）
| A． | $\sqrt{5}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{5}}{2}$ |