题目内容
15．函数y=loga（2x-3）+$\frac{\sqrt{2}}{2}$的图象恒过定点P，P在幂函数f（x）的图象上，则f（9）=（ ）| A． | $\frac{1}{3}$ | B． | $\sqrt{3}$ | C． | 3 | D． | 9 |
分析 由题意求出点P的坐标，代入f（x）求函数解析式，再将9代入即可．
解答 解：由题意，令2x-3=1，则y=$\frac{\sqrt{2}}{2}$，
即点P（2，$\frac{\sqrt{2}}{2}$），
由P在幂函数（x）=xα的图象上可得，2α=$\frac{\sqrt{2}}{2}$
则α=-$\frac{1}{2}$，
则f（x）=${x}^{-\frac{1}{2}}$
则f（9）=$\frac{1}{3}$，
故选A．
点评 本题考查了对数函数与幂函数的性质应用，属于基础题．
练习册系列答案
相关题目
5．
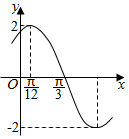函数$f（x）=Asin（{ωx+ϕ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，
求（Ⅰ）函数f（x）的解析式；
（Ⅱ）函数y=Acos（ωx+ϕ）的单调递增区间．
函数$f（x）=Asin（{ωx+ϕ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，求（Ⅰ）函数f（x）的解析式；
（Ⅱ）函数y=Acos（ωx+ϕ）的单调递增区间．
20．等差数列{an}中，a1=2，公差d=3则{an}的通项公式为（ ）
| A． | .an=3n-1 | B． | an=2n+1 | C． | .an=2n+3 | D． | .an=3n+2 |
