题目内容
4.如图所示,在一半径等于1千米的圆弧及直线段道路AB围成的区域内计划建一条商业街,其起点和终点均在道路AB上,街道由两条平行于对称轴l且关于l对称的两线段EF、CD,及夹在两线段EF、CD间的弧组成.若商业街在两线段EF、CD上收益为每千米2a元,在两线段EF、CD间的弧上收益为每千米a元.已知$∠AOB=\frac{π}{2}$,设∠EOD=2θ,(1)将商业街的总收益f(θ)表示为θ的函数;
(2)求商业街的总收益的最大值.
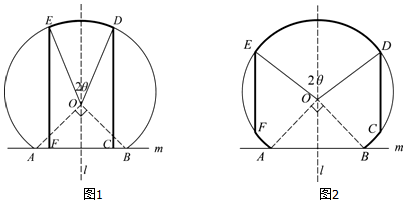
分析 (1)①求出θ∈(0,$\frac{π}{4}$]时f(θ)的解析式;
②求出θ∈($\frac{π}{4}$,$\frac{π}{2}$)时f(θ)的解析式,
利用分段函数写出f(θ)在(0,$\frac{π}{2}$)上的解析式;
(2)利用导数研究函数f(θ)在(0,$\frac{π}{2}$)上的单调性并求出最大值.
解答 解:(1)①当θ∈(0,$\frac{π}{4}$]时,ED=2θ,EF=$\frac{\sqrt{2}}{2}$+cosθ;
∴f(θ)=2aθ+2a($\sqrt{2}$+2cosθ);
②当θ∈($\frac{π}{4}$,$\frac{π}{2}$)时,ED+FA+BC=4θ-$\frac{π}{2}$,EF=2cosθ;
∴f(θ)=(4θ-$\frac{π}{2}$)a+2a(4cosθ);
由①②可得,f(θ)=$\left\{\begin{array}{l}{2a(θ+\sqrt{2}+2cosθ),θ∈(0,\frac{π}{4}]}\\{a(4θ-\frac{π}{4}+8cosθ),θ∈(\frac{π}{4},\frac{π}{2})}\end{array}\right.$;
(2)①当θ∈(0,$\frac{π}{4}$]时,f′(θ)=2a(1-2sinθ);
由a>0,填表如下:
| θ | (0,$\frac{π}{6}$] | $\frac{π}{6}$ | ($\frac{π}{6}$,$\frac{π}{4}$) |
| f′(θ) | + | 0 | - |
| f(θ) | 单调递增 | 极大值 | 单调递减 |
②当θ∈($\frac{π}{4}$,$\frac{π}{2}$)时,f′(θ)=a(4-8sinθ);
∵a>0,且sinθ∈($\frac{\sqrt{2}}{2}$,1),
∴f′(θ)=a(4-8sinθ)<0,
∴f(θ)在θ∈($\frac{π}{4}$,$\frac{π}{2}$)时单调递减,
∴f(θ)<f($\frac{π}{4}$);
又∵f($\frac{π}{4}$)<f($\frac{π}{6}$),
∴当θ∈(0,$\frac{π}{2}$)时,在θ=$\frac{π}{6}$时f(θ)取得最大值为(2$\sqrt{2}$+2$\sqrt{3}$+$\frac{π}{3}$)a;
即θ=$\frac{π}{6}$时,商业街总收益最大,最大值为(2$\sqrt{2}$+2$\sqrt{3}$+$\frac{π}{3}$)a.
点评 本题考查了三角函数模型的应用问题,也考查了用导数研究函数的单调性与最值问题,是难题.

练习册系列答案
相关题目
14.给出下列命题:①向量$\overrightarrow{AB}$与$\overrightarrow{BA}$是相等向量;②共线的单位向量是相等向量;③模为零的向量与任一向量共线;④两平行向量所在直线互相平行.其中不正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
15.函数y=loga(2x-3)+$\frac{\sqrt{2}}{2}$的图象恒过定点P,P在幂函数f(x)的图象上,则f(9)=( )
| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
12.等差数列有如下性质:若数列{an}为等差数列,则当${b_n}=\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$时,数列{bn}也是等差数列;类比上述性质,相应地,若数列{cn}是正项等比数列,当dn=____________时,数列{dn}也是等比数列,则dn的表达式为( )
| A. | ${d_n}=\frac{{{c_1}+{c_2}+…+{c_n}}}{n}$ | B. | ${d_n}=\frac{{{c_1}•{c_2}{•_{\;}}{…_{\;}}•{c_n}}}{n}$ | ||
| C. | ${d_n}=\root{n}{{{c_1}•{c_2}{•_{\;}}{…_{\;}}•{c_n}}}$ | D. | ${d_n}=\root{n}{{\frac{{{c_1}^n•{c_2}^n{•_{\;}}{…_{\;}}•{c_n}^n}}{n}}}$ |
19.已知“x>k”是“$\frac{3}{x+1}<1$”的充分不必要条件,则k的取值范围为( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | [2,+∞) | D. | (2,+∞) |