题目内容
3.在△ABC中,角A、B、C的对边分别为a、b、c,满足b2+c2=a2+bc.(1)求角A的大小;
(2)求$y=\sqrt{3}sinB+cosB$的值域.
分析 (1)利用余弦定理转化求解即可.
(2)通过两角和与差的三角函数化简函数的解析式,通过B的范围,求解函数的最值即可.
解答 解:(1)由题意得,b2+c2-a2=bc
则$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$,且A∈(0,π),所以$A=\frac{π}{3}$.
(2)原式化为$y=2sin(B+\frac{π}{6})$,$B∈(0,\frac{2π}{3})$$B+\frac{π}{6}∈(\frac{π}{6},\frac{5π}{6})$,$sin(B+\frac{π}{6})∈(\frac{1}{2},\left.1]$,
故值域为(1,2].
点评 本题考查余弦定理的应用,两角和与差的三角函数,三角函数的最值的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知函数$f(x)=\frac{1}{2}{x^3}+ax-b$在区间[-1,1]上为增函数,则在区间[0,1]上任意取两个实数a,b,使f(x)在区间[-1,1]上有且仅有一个零点的概率为( )
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
11.已知$\overrightarrow a=(2,1)$,$\overrightarrow b=(3,-2)$,则 $\overrightarrow a•\overrightarrow b$的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
8.下列函数中是偶函数的有( )
| A. | y=x2 | B. | y=x | C. | y=x3 | D. | y=2x |
12.($\sqrt{x}+\frac{1}{2\sqrt{x}}$)8的展开式中常数项为( )
| A. | $\frac{35}{16}$ | B. | $\frac{35}{8}$ | C. | $\frac{35}{4}$ | D. | 105 |
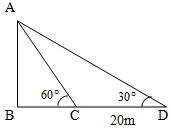 如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为$10\sqrt{3}$米.
如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为$10\sqrt{3}$米.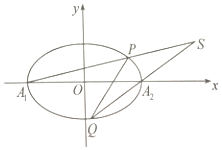 已知椭圆C的离心率为$e=\frac{{\sqrt{2}}}{2}$,长轴的左、右端点分别为A1(-2,0),A2(-2,0).
已知椭圆C的离心率为$e=\frac{{\sqrt{2}}}{2}$,长轴的左、右端点分别为A1(-2,0),A2(-2,0).