题目内容
比较1+logx3与2logx2(x>0且x≠1)的大小.
【答案】分析:由于要比较的两个数都是对数,我们联系到对数的性质,以及对数函数的单调性,讨论即可.
解答:解:(1+logx3)-2logx2=logx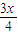 .
.
当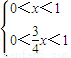 或
或
即0<x<1或x> 时,
时,
有logx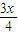 >0,1+logx3>2logx2.
>0,1+logx3>2logx2.
当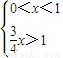 ①或
①或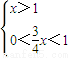 ②时,logx
②时,logx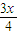 <0.
<0.
解①得无解,解②得1<x< ,
,
即当1<x< 时,有logx
时,有logx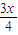 <0,
<0,
1+logx3<2logx2.
当 x=1,即x=
x=1,即x= 时,有logx
时,有logx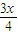 =0.
=0.
∴1+logx3=2logx2.
综上所述,当0<x<1或x> 时,1+logx3>2logx2;
时,1+logx3>2logx2;
当1<x< 时,1+logx3<2logx2;
时,1+logx3<2logx2;
当x= 时,1+logx3=2logx2.
时,1+logx3=2logx2.
点评:本题考查对数函数的性质,作差法,分类讨论的思想,是中档题.
解答:解:(1+logx3)-2logx2=logx
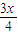 .
.当
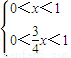 或
或
即0<x<1或x>
 时,
时,有logx
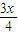 >0,1+logx3>2logx2.
>0,1+logx3>2logx2.当
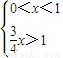 ①或
①或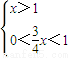 ②时,logx
②时,logx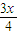 <0.
<0.解①得无解,解②得1<x<
 ,
,即当1<x<
 时,有logx
时,有logx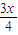 <0,
<0,1+logx3<2logx2.
当
 x=1,即x=
x=1,即x= 时,有logx
时,有logx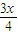 =0.
=0.∴1+logx3=2logx2.
综上所述,当0<x<1或x>
 时,1+logx3>2logx2;
时,1+logx3>2logx2;当1<x<
 时,1+logx3<2logx2;
时,1+logx3<2logx2;当x=
 时,1+logx3=2logx2.
时,1+logx3=2logx2.点评:本题考查对数函数的性质,作差法,分类讨论的思想,是中档题.

练习册系列答案
相关题目