题目内容

设x＞0，且x≠1，比较1+logx3与2logx2的大小.

0＜x＜1或x＞时，1+logx3＞2logx2；

当1＜x＜时,1+logx3＜2logx2；

当x=时，1+logx3=2logx2.


解析:

(1+logx3)－2logx2=logx3x－logx4=logx.

①当0＜x＜1，

或当x＞时，

有logx＞0,即1+logx3＞2logx2；

②当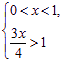或1＜x＜时，

logx＜0,即1+logx3＜2logx2；

③当=1x=时，logx=0,

即2logx2=1+logx3.

综上所述,当0＜x＜1或x＞时，1+logx3＞2logx2；

当1＜x＜时,1+logx3＜2logx2；

当x=时，1+logx3=2logx2.

练习册系列答案
相关题目
设函数f（x）=ax3+bx2+cx+d（a、b、c、d∈R）满足：?x∈R都有f（x）+f（-x）=0，且x=1时，f（x）取极小值-
2
3
．
（1）f（x）的解析式；
（2）当x∈[-1，1]时，证明：函数图象上任意两点处的切线不可能互相垂直：
（3）设F（x）=|xf（x）|，证明：x∈(0，
3
)时，F(x)≤
3
4
．
对于给定的n项数列S={a1，a2，…，an}，令f（S）为n-1项数列{
a1+a2
2
，
a2+a3
2
，…，
an-1+an
2
}；设x＞0，且S={1，x，x2，…，x100}，若
ff…f
100个
(S)={
1
250
}，则x的值为（　　）
设函数f（x）=ax3+bx2+cx+d（a、b、c、d∈R）满足：对于任意的x∈R都有f（x）+f（-x）=0，且x=1时f（x）取极小值-
23
．
（1）f（x）的解析式；
（2）当x∈[-1，1]时，证明：函数图象上任意两点处的切线不可能互相垂直：
（2013•日照一模）给出下列四个命题：
①若x＞0，且x≠1则lgx+
1
lgx
≥2；
②设x，y∈R，命题“若xy=0，则x2+y2=0”的否命题是真命题；
③若函数y=f（x）的图象在点M（1，f（1））处的切线方程是y=
1
2
x+2，则f（1）+f'（1）=3；
④已知抛物线y2=4px（p＞0）的焦点F与双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点重合，点A是两曲线的交点，AF⊥x轴，则双曲线的离心率为
2
+1．
其中所有真命题的序号是
②③④
②③④
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网