题目内容
化简:(log49+log163)(log92+log34)= .
考点:对数的运算性质
专题:函数的性质及应用
分析:根据对数的运算性质计算即可
解答:
解:(log49+log163)(log92+log34)
=log49•log92+log49•log34+log163•log92+log163•log34
=log42+log39+log162•log93+log164
=
+2+
×
+
=
故答案为:
=log49•log92+log49•log34+log163•log92+log163•log34
=log42+log39+log162•log93+log164
=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 25 |
| 8 |
故答案为:
| 25 |
| 8 |
点评:本题考查了对数的运算性质,属于基础题

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知cosαcosβ-sinαsinβ=0,那么sinαcosβ+cosαsinβ的值为(
| A、-1 | B、0 | C、1 | D、±1 |
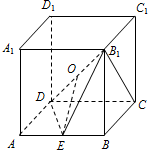 如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.