题目内容
函数y=x2(x>0)的图象在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,k为正整数,a1=16,则an=分析:在点(ak,ak2)处的切线方程为:y-ak2=2ak(x-ak),当y=0时,解得x=
,所以ak+1=
,再由a1=16,能够求出an.
| ak |
| 2 |
| ak |
| 2 |
解答:解:函数y=x2(x>0)在点(ak,ak2)处的切线方程为:y-ak2=2ak(x-ak),
当y=0时,解得 x=
,
所以 ak+1=
,即
=
,
∵a1=16,∴an=16×(
)n-1.
故答案为:16×(
)n-1.
当y=0时,解得 x=
| ak |
| 2 |
所以 ak+1=
| ak |
| 2 |
| ak+1 |
| ak |
| 1 |
| 2 |
∵a1=16,∴an=16×(
| 1 |
| 2 |
故答案为:16×(
| 1 |
| 2 |
点评:本题考查数列的性质和应用,解题时要灵活地运用函数的切线方程,合理地进行等价转换.

练习册系列答案
相关题目
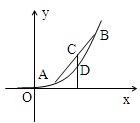 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).