题目内容
对于平面直角坐标系内的任意两点 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: .给出下列三个命题:
.给出下列三个命题:
①若点C在线段AB上,则 ;
;
②在 中,若∠C=90°,则
中,若∠C=90°,则 ;
;
③在 中,
中, .
.
其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:①若点C在线段AB上,设点C(x0,y0)那么x0在x1,x2之间.y0在y1,y2之间,所以||AC||+||CB||=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|=|x2-x1|+|y2-y1|=||AB||正确;
②平方后不能消除x0,y0,命题不成立;
③不妨假设C角为直角,以A为原点,AC所在直线为x轴,作直角坐标,得A(0 , 0 )、B( ),点C(
),点C( ,0)。代入③式中得:︱
,0)。代入③式中得:︱ ︱+︱
︱+︱ ︱=︱
︱=︱ ︱+︱
︱+︱ ︱,所以③不成立。故选B.
︱,所以③不成立。故选B.
考点:本题考查两点间的距离公式。
点评:本题是新运算与绝对值的结合,应注意点C的不同位置。弄清新命题的运算规则,是本题的关键点;设出各点坐标,代入关系式计算,根据计算结果进行判断是做本题的基本前提。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
经过点P(4,-2)的抛物线标准方程为( )
| A.y2=x或x2=-8y | B.y2=x或y2=8x |
| C.y2=-8x | D.x2=-8y |
曲线y=1+ 与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
A.(0, ) ) | B.( ,+∞) ,+∞) |
C.( , , ] ] | D.( , , ] ] |
若直线 和⊙O:
和⊙O: 没有交点,则过
没有交点,则过 的直线与椭圆
的直线与椭圆 的交点个数 ( )
的交点个数 ( )
| A.至多一个 | B.0个 | C.1个 | D.2个 |
已知圆锥曲线 的离心率e为方程
的离心率e为方程 的两根,则满足条件的圆锥曲线的条数为 ( )
的两根,则满足条件的圆锥曲线的条数为 ( )
| A.1 | B.2 | C.3 | D.4 |
若点 和点
和点 分别为双曲线
分别为双曲线 (
( )的中心和左焦点,点
)的中心和左焦点,点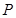 为双曲线右支上的任意一点,则
为双曲线右支上的任意一点,则 的取值范围为( )
的取值范围为( )
A.[3-  , ,  ) ) | B.[3+  , ,  ) ) |
C.[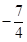 , ,  ) ) | D.[ , ,  ) ) |
 (
( )的两焦点分别为
)的两焦点分别为 、
、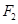 ,以
,以
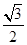


 的两焦点为
的两焦点为 、
、 ,以
,以 为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )



 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )