题目内容
若点 和点
和点 分别为双曲线
分别为双曲线 (
( )的中心和左焦点,点
)的中心和左焦点,点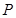 为双曲线右支上的任意一点,则
为双曲线右支上的任意一点,则 的取值范围为( )
的取值范围为( )
A.[3-  , ,  ) ) | B.[3+  , ,  ) ) |
C.[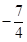 , ,  ) ) | D.[ , ,  ) ) |
B
解析试题分析: 因为F(-2,0)是已知双曲线的左焦点,所以a2+1=4,即a2=3,所以双曲线方程为 设点P(x0,y0),则有
设点P(x0,y0),则有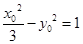 (x0≥
(x0≥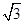 ),解得y02=
),解得y02= (x0≥
(x0≥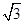 ),
),
因为 =(x0+2,y0),
=(x0+2,y0),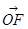 =(x0,y0),所以
=(x0,y0),所以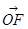
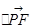 =x0(x0+2)+y02=x0(x0+2)+
=x0(x0+2)+y02=x0(x0+2)+ =
= +2x0-1,此二次函数对应的抛物线的对称轴为x0=-
+2x0-1,此二次函数对应的抛物线的对称轴为x0=-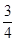 ,因为x0≥
,因为x0≥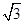 ,
,
所以当x0=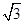 时,
时,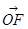
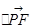 取得最小值
取得最小值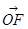
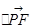 =
= ,故
,故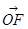
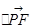
的取值范围是[ ,+∞),选B
,+∞),选B
考点:本题主要考查了待定系数法求双曲线方程,考查平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程度以及知识的综合应用能力、运算能力.
点评:解决该试题的关键是先根据双曲线的焦点和方程中的b求得a,则双曲线的方程可得,设出点P,代入双曲线方程求得y0的表达式,根据P,F,O的坐标表示出 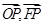 ,进而求得
,进而求得  的表达式,利用二次函数的性质求得其最小值,则
的表达式,利用二次函数的性质求得其最小值,则 的取值范围可得.
的取值范围可得.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
已知椭圆 的长轴长为10,离心率
的长轴长为10,离心率 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. 或 或 | B. 或 或 |
C. 或 或 | D. 或 或 |
双曲线 上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
| A.1或13 | B.15 | C.13 | D.1 |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
设直线 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 与椭圆
与椭圆 的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为
的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为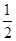 的点M的个数为
的点M的个数为
| A.1 | B.2 | C.3 | D.4 |
以椭圆 的焦点为顶点、顶点为焦点的的双曲线方程是
的焦点为顶点、顶点为焦点的的双曲线方程是
A. | B. |
C. | D. |
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点,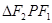 是底角为
是底角为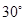 的等腰三角形,则
的等腰三角形,则 的离心率为 ( )
的离心率为 ( )
A. | B. | C. | D. |
 (a>0,b>0)的一条渐近线方程是y=
(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )



 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: .给出下列三个命题:
.给出下列三个命题: ;
; 中,若∠C=90°,则
中,若∠C=90°,则 ;
; .
.