题目内容
5.点B,F分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点与左焦点,过F作x轴的垂线与椭圆交于第二象限的一点P,H($\frac{{a}^{2}}{c}$,0)(c为半焦距),若OP∥BH(O为坐标原点),则椭圆的离心率为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\sqrt{\frac{\sqrt{5}-1}{2}}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{{\;}^{3}\sqrt{4}}{2}$ |
分析 依题意,可求得P(-c,$\frac{{b}^{2}}{a}$),利用HB∥OP求得c2=ab,再利用椭圆的性质即可求得答案.
解答 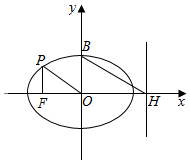 解:依题意,作图如下:
解:依题意,作图如下:
∵F(-c,0)是椭圆的左焦点,PF⊥OF,
∴P(-c,$\frac{{b}^{2}}{a}$),
∴直线OP的斜率k=$\frac{\frac{{b}^{2}}{a}-0}{-c-0}=-\frac{{b}^{2}}{ac}$;
又H($\frac{{a}^{2}}{c}$,0),B(0,b),
∴直线HB的斜率k′=$\frac{b-0}{0-\frac{{a}^{2}}{c}}=-\frac{bc}{{a}^{2}}$.
∵HB∥OP,
∴$-\frac{{b}^{2}}{ac}=-\frac{bc}{{a}^{2}}$,
∴c2=ab,又b2=a2-c2,
∴c4=a2b2=a2(a2-c2),
∴e4+e2-1=0,
∴e2=$\frac{\sqrt{5}-1}{2}$,
则e=$\sqrt{\frac{\sqrt{5}-1}{2}}$,
故选:B.
点评 本题考查椭圆的性质,利用HB∥OP求得c2=ab是关键,考查分析与计算能力,属于中档题.

练习册系列答案
相关题目
16.设集合S={x|x>1},T={x||x-1|≤2},则(∁RS)∪T( )
| A. | (-∞,3] | B. | [-1,1] | C. | [-1,3] | D. | [-1,+∞) |
20.把1011011(2)转化成十进制数为( )
| A. | 88 | B. | 89 | C. | 90 | D. | 91 |