题目内容
12.已知△ABC外接圆的圆心为O,且$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,则$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 可由$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$得出点O为边BC的中点,从而得出边BC为△ABC外接圆的直径,从而得出$∠BAC=\frac{π}{2}$,这样即可得出$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角.
解答 解:如图,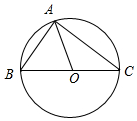
∵$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$;
∴圆心O为BC边的中点;
∴BC为外接圆的直径;
∴$∠BAC=\frac{π}{2}$;
即$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为$\frac{π}{2}$.
故选:D.
点评 考查向量加法的平行四边形法则,圆的直径过圆心,以及直径所对的圆周角为直角,向量夹角的概念.

练习册系列答案
相关题目
7.已知函数f(x)=(ex+1)(ax+2a-2),若存在x∈(0,+∞),使得不等式f(x)-2<0成立,则实数a的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{3}{2}$) | C. | (-∞,1) | D. | (-∞,$\frac{4}{3}$) |
4.已知直线l1:mx+y-2=0,l2:6x+(2m-1)y-6=0,若l1∥l2,则实数m的值是( )
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{3}{2}$或-2 | D. | $\frac{3}{2}$或-2 |