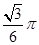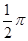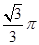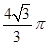题目内容
已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）
A． | B． |
C． | D． |
B
解析试题分析：由三视图可得几何体是四棱锥V-ABCD，
其中面VCD⊥面ABCD；
底面ABCD是边长为20cm的正方形；棱锥的高是20cm
由棱锥的体积公式得V=
=
.
考点：由三视图求面积、体积．
点评：三视图是新增考点，根据三张图的关系，可知几何体是正方体的一部分，是一个四棱锥．本题也可改编为求该几何体的外接球的表面积，则必须补全为正方体，增加了难度．
练习册系列答案
名校课堂系列答案
相关题目
某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A．18 | B．21 | C．24 | D．27 |
的底面边长为
，高
，点
在高
上，且
，记过点
的球的半径为
，则函数
几何体的三视图如图，则几何体的体积为
A． | B． | C． | D． |
下图表示一个几何体的三视图及相应数据，则该几何体的体积是
A． | B． | C． | D． |
的棱长为1，动点P在此正方体的表面上运动，且
，记点P的轨迹的长度为
，则函数的图像
某四棱锥的三视图如图所示，该四棱锥的表面积是（ ）
A． | B． | C． | D． |
三棱锥
中，
是底面，
且这四个顶点都在半径为2的球面上，
则这个三棱锥的三个侧棱长的和的最大值为（ ）
| A．16 | B． | C． | D．32 |
