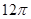题目内容
几何体的三视图如图，则几何体的体积为
A． | B． | C． | D． |
D
解析试题分析：根据三视图的特征可知该几何体为圆柱与圆锥的组合体，圆柱的底面圆直径为2，高为1，圆锥底面圆直径为2，高为1，根据柱体椎体的体积公式可知该几何体的体积为
考点：三视图及几何体体积
点评：先由三视图的特征结合各种常见几何体找到与三视图对应的几何体，再代入相应的体积公式计算
练习册系列答案
相关题目
一个棱锥的三视图如图，则该棱锥的表面积（单位：c
）为（ ）
A．48+12 | B．48+24 | C．36+12 | D．36+24 |
一个几何体的三视图如图所示，其中俯视图为正三角形，则侧视图的面积为
| A．8 | B． | C． | D．4 |
某几何体的三视图如图所示，则该几何体的体积不可能是（ ）
A． | B． | C． | D． |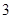
如图所示，在正方体ABCD-A1B1C1D1中，E，F分别为棱AA1，CC1的中点，则在空间中与直线A1D1，EF，CD都相交的直线( )．
| A．有无数条 | B．有且只有两条 | C．有且只有三条 | D．不存在 |
某空间几何体的三视图及尺寸如图1，则该几何体的体积是
A． | B． | C． | D． |
在正三棱柱
中，若AB=2，
则点A到平面
的距离为（ ）
A． | B． | C． | D． |
