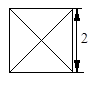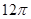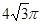题目内容
三棱锥
中，
是底面，
且这四个顶点都在半径为2的球面上，
则这个三棱锥的三个侧棱长的和的最大值为（ ）
| A．16 | B． | C． | D．32 |
B
解析试题分析：∴PA，PB，PC两两垂直，又∵三棱锥P-ABC的四个顶点均在半径为1的球面上，∴以PA，PB，PC为棱的长方体的对角线即为球的一条直径．∴16=PA2+PB2+PC2，因为则这个三棱锥的三个侧棱长的和
,则借助于二次函数的性质可知其最大值为，选B.
考点：棱锥的侧棱长和最值
点评：本题考查的知识点是棱锥的侧棱长和，基本不等式，棱柱的外接球，其中根据已知条件，得到棱锥的外接球直径等于以PA，PB，PC为棱的长方体的对角线，是解答本题的关键．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
一个几何体的三视图如图所示，其中俯视图为正三角形，则侧视图的面积为
| A．8 | B． | C． | D．4 |
在正三棱柱
中，若AB=2，
则点A到平面
的距离为（ ）
A． | B． | C． | D． |
已知正三角形ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为( )
A． a2 | B． a2 | C． a2 | D． a2 |
已知一个空间几何体的三视图如图所示，则这个几何体的表面积是
A． | B． | C． | D． |
的正方形，主视图与左视图是边长为
