题目内容
如图,已知正方体 的棱长为1,动点P在此正方体的表面上运动,且
的棱长为1,动点P在此正方体的表面上运动,且 ,记点P的轨迹的长度为
,记点P的轨迹的长度为 ,则函数的图像
,则函数的图像 可能是( )
可能是( )

B
解析试题分析:P的轨迹为以A为球心,PA为半径的球面与正方体的交线。所以在 时,轨迹长度直线增加,而
时,轨迹长度直线增加,而 时,轨迹长度由减小到增加,之后逐渐减小,故选B。
时,轨迹长度由减小到增加,之后逐渐减小,故选B。
考点:本题主要考查正方体、球的几何特征,轨迹的概念。
点评:中档题,解题的关键是认识到P的轨迹为以A为球心,PA为半径的球面与正方体的交线。定性分析“交线”的长度变化规律。

练习册系列答案
相关题目
某几何体的三视图如图所示,则其侧面积为( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则该几何体的体积不可能是( )
A. | B. | C. | D.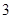 |
某空间几何体的三视图及尺寸如图1,则该几何体的体积是
A. | B. | C. | D. |
以下对于几何体的描述,错误的是( )
| A.以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球 |
| B.一个等腰三角形绕着底边上的高所在直线旋转180º形成的封闭曲面所围成的图形叫做圆锥 |
| C.用平面去截圆锥,底面与截面之间的部分叫做圆台 |
| D.以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱 |
在正三棱柱 中,若AB=2,
中,若AB=2, 则点A到平面
则点A到平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
已知一个空间几何体的三视图如图所示,则这个几何体的表面积是
A. | B. | C. | D. |









