题目内容
已知函数f(x)=ex,g(x)=ln(x+m).直线l:y=kx+b经过点P(-1,0)且与曲线y=f(x)相切.
(1)求切线l的方程.
(2)若关于x的不等式kx+b≥g(x)恒成立,求实数m的最大值.
(3)设F(x)=f(x)-g(x),若函数F(x)有唯一的零点x0,求证-1<x0<-
.
(1)求切线l的方程.
(2)若关于x的不等式kx+b≥g(x)恒成立,求实数m的最大值.
(3)设F(x)=f(x)-g(x),若函数F(x)有唯一的零点x0,求证-1<x0<-
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)设切点为(x1,y1),求出切点坐标,即可求切线l的方程.
(2)设h(x)=1+x-ln(x+m),求导数,确定函数的单调性,求出最值,即可求实数m的最大值.
(3)函数F(x)有唯一的零点x0,可知f(x)=ex,g(x)=ln(x+m)在(x0,y0)处有公共切线l,可得ex0+x0=0,设H(x)=ex+x,证明H(x)在(-m,+∞)上单调递增,即可得出结论.
(2)设h(x)=1+x-ln(x+m),求导数,确定函数的单调性,求出最值,即可求实数m的最大值.
(3)函数F(x)有唯一的零点x0,可知f(x)=ex,g(x)=ln(x+m)在(x0,y0)处有公共切线l,可得ex0+x0=0,设H(x)=ex+x,证明H(x)在(-m,+∞)上单调递增,即可得出结论.
解答:
(1)解:设切点为(x1,y1),则
∵f(x)=ex,∴f′(x)=ex,
∴切线l:y-ex1=ex1(x-x1),
P(-1,0)代入可得0-ex1=ex1(-1-x1),
∴x1=0,
∴切线l:y=x+1;
(2)设h(x)=1+x-ln(x+m),则h′(x)=
,
∴-m<x<1-m时,h′(x)<0,x>1-m时,h′(x)>0,
∴h(x)在x=1-m时取极小值,也是最小值,
∵关于x的不等式kx+b≥g(x)恒成立,
∴h(1-m)=2-m≥0,
∴m≤2,
∴实数m的最大值为2.
(3)证明:由题意,方程ex=ln(x+m)有唯一实根x0,
即f(x)=ex,g(x)=ln(x+m)有唯一交点,图象如图所示,

可知f(x)=ex,g(x)=ln(x+m)在(x0,y0)处有公共切线l,
∴ex0=
,
∴ex0+x0=0,
设H(x)=ex+x,则H′(x)=ex+1>0,
∴H(x)在(-m,+∞)上单调递增,
∵H(-
)=e-
-
>0,H(-1)=
-1<0,
∴-1<x0<-
.
∵f(x)=ex,∴f′(x)=ex,
∴切线l:y-ex1=ex1(x-x1),
P(-1,0)代入可得0-ex1=ex1(-1-x1),
∴x1=0,
∴切线l:y=x+1;
(2)设h(x)=1+x-ln(x+m),则h′(x)=
| x+m-1 |
| x+m |
∴-m<x<1-m时,h′(x)<0,x>1-m时,h′(x)>0,
∴h(x)在x=1-m时取极小值,也是最小值,
∵关于x的不等式kx+b≥g(x)恒成立,
∴h(1-m)=2-m≥0,
∴m≤2,
∴实数m的最大值为2.
(3)证明:由题意,方程ex=ln(x+m)有唯一实根x0,
即f(x)=ex,g(x)=ln(x+m)有唯一交点,图象如图所示,

可知f(x)=ex,g(x)=ln(x+m)在(x0,y0)处有公共切线l,
∴ex0=
| 1 |
| x0+m |
∴ex0+x0=0,
设H(x)=ex+x,则H′(x)=ex+1>0,
∴H(x)在(-m,+∞)上单调递增,
∵H(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| e |
∴-1<x0<-
| 1 |
| 2 |
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查函数的最值,考查学生分析解决问题的能力,正确求导是关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
如图所给的程序运行结果为S=35,那么判断框中应填入的关于k的条件是( )


| A、k=7 | B、k≤6 |
| C、k<6 | D、k>6 |
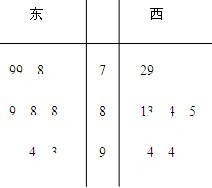 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.