题目内容
11.圆x2+y2-4x=0的圆心坐标和半径分别为( )| A. | (2,0),4 | B. | (2,0),2 | C. | (-2,0),4 | D. | (-2,0),2 |
分析 把圆的方程利用配方法化为标准方程后,即可得到圆心与半径.
解答 解:圆x2+y2-4x=0可化为(x-2)2+y2=4,
∴圆x2+y2-4x=0的圆心坐标和半径分别为(2,0),2,
故选:B.
点评 此题比较简单,要求学生会把圆的一般方程化为标准方程.

练习册系列答案
相关题目
19.已知y=f(x)为(0,+∞)上的可导函数,且(x+1)f′(x)>f(x),则以下一定成立的是( )
| A. | 3f(4)<4f(3) | B. | 3f(4)>4f(3) | C. | 3f(3)<4f(2) | D. | 3f(3)>4f(2) |
1.若函数f(x)=x2-bx+3(b为实数)的最小值是-1,则f(x)的图象的对称轴方程( )
| A. | x=1 | B. | x=2 | C. | x=-1或x=1 | D. | x=-2或x=2 |
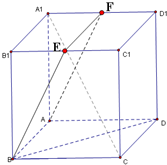 在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.
在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.