题目内容
已知函数f(x)=lnx-ax+2在点(1,f(1))处的切线与直线l:x-y-1=0垂直,
(1)求实数a的值和函数f(x)的单调区间;
(2)若g(n)=1+
+
+…+
,h(n)=lnn,数列{an}:an=2g(n)-h(n),求实数m的取值范围,使对任意n∈N*,不等式an>log2m-4logm2-1恒成立.
(1)求实数a的值和函数f(x)的单调区间;
(2)若g(n)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
考点:函数恒成立问题,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)求函数的导数,根据导数的几何意义,以及切线关系即可,求实数a的值和函数f(x)的单调区间;
(2)求出数列的通项公式,将不等式恒成立进行转化,利用参数分离法即可得到结论.
(2)求出数列的通项公式,将不等式恒成立进行转化,利用参数分离法即可得到结论.
解答:
解:(1)由已知f′(x)=
-a,f′(1)=1-a=-1,
∴a=2.
由f′(x)=
-2>0,解得0<x<
,
由f′(x)=
-2<0,解得x>
.
∴函数f(x)的单调递增区间是(0,
),单调递减区间是(
,+∞).
(2)由已知an=2g(n)-lnn=2(1+
+
+…+
)-lnnan+1=2(1+
+
+…+
)-ln(n+1),
∴an+1-an=
+lnn-ln(n+1)=ln
-
+2,
由(1)知函数f(x)在区间[
,1]上单调递减
由于
≤
<1,∴ln
-
+2=f(
)>f(1)=0即an+1>an.
∴log2m-4logm2-1<(an)min=a1=2,
解得
<m<16且m≠1.
∴实数m的取值范围是(
,1)∪(1,16).
| 1 |
| x |
∴a=2.
由f′(x)=
| 1 |
| x |
| 1 |
| 2 |
由f′(x)=
| 1 |
| x |
| 1 |
| 2 |
∴函数f(x)的单调递增区间是(0,
| 1 |
| 2 |
| 1 |
| 2 |
(2)由已知an=2g(n)-lnn=2(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
∴an+1-an=
| 2 |
| n+1 |
| n |
| n+1 |
| 2n |
| n+1 |
由(1)知函数f(x)在区间[
| 1 |
| 2 |
由于
| 1 |
| 2 |
| n |
| n+1 |
| n |
| n+1 |
| 2n |
| n+1 |
| n |
| n+1 |
∴log2m-4logm2-1<(an)min=a1=2,
解得
| 1 |
| 2 |
∴实数m的取值范围是(
| 1 |
| 2 |
点评:本题主要考查导数的几何意义以及函数单调性和导数之间的关系,将不等式恒成立进行转化,利用数列的单调性是解决本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 2014年春节期间,高速公路车辆剧增,高速公路管理测控中心在一特定位置从七座以下小型汽车中按先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆进行电子测速调查,将它们的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如图的频率分布直图.
2014年春节期间,高速公路车辆剧增,高速公路管理测控中心在一特定位置从七座以下小型汽车中按先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆进行电子测速调查,将它们的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如图的频率分布直图.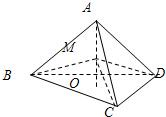 如图,已知AO是四面体ABCD的高,M是AO的中点,连接BM、CM、DM.求证:BM、CM、DM两两垂直.
如图,已知AO是四面体ABCD的高,M是AO的中点,连接BM、CM、DM.求证:BM、CM、DM两两垂直.