题目内容
已知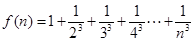 ,
, ,
,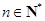 .
.
(1)当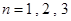 时,试比较
时,试比较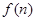 与
与 的大小关系;
的大小关系;
(2)猜想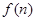 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
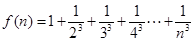 ,
, ,
,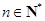 .
.(1)当
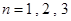 时,试比较
时,试比较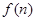 与
与 的大小关系;
的大小关系;(2)猜想
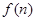 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.(1) ,
, ,
, ;(2)猜想:对一切
;(2)猜想:对一切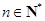 ,
, ,证明详见解析.
,证明详见解析.
 ,
, ,
, ;(2)猜想:对一切
;(2)猜想:对一切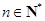 ,
, ,证明详见解析.
,证明详见解析.试题分析:(1)由
 的公式分别计算出
的公式分别计算出 时的
时的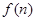 及
及 的值,进而可得比较它们的大小关系;(2)用数学归纳法证明,由(1)可知,
的值,进而可得比较它们的大小关系;(2)用数学归纳法证明,由(1)可知, 时,不等式显然成立,接着假设
时,不等式显然成立,接着假设 时不等式成立,进而只须证明
时不等式成立,进而只须证明 时不等式也成立即可,在证明
时不等式也成立即可,在证明 时,又只须将
时,又只须将 变形为
变形为 ,之后只须用比较法比较判断
,之后只须用比较法比较判断 与
与 大小,即可证明本题.
大小,即可证明本题.(1) 当
 时,
时, ,
, ,所以
,所以 1分
1分当
 时,
时, ,
, ,所以
,所以 2分
2分当
 时,
时, ,
, ,所以
,所以 4分
4分(2) 由(1),猜想
 ,下面用数学归纳法给出证明 6分
,下面用数学归纳法给出证明 6分①当
 时,不等式显然成立 7分
时,不等式显然成立 7分②假设当
 时不等式成立,即
时不等式成立,即 9分
9分那么,当
 时,
时,  11分
11分因为
 14分
14分所以
 15分
15分由①、②可知,对一切
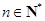 ,都有
,都有 成立 16分.
成立 16分.
练习册系列答案
相关题目

 行中所有数的和为 。
行中所有数的和为 。
 使得
使得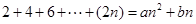 对一切
对一切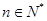 恒成立?若存在,求出
恒成立?若存在,求出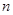 条直线,其中任何两条不平行,任何三条不共点,当
条直线,其中任何两条不平行,任何三条不共点,当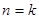 时把平面分成的区域数记为
时把平面分成的区域数记为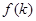 ,则
,则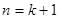 时
时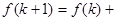 .
. ,则n=k+1时左端在n=k时的左端加上________.
,则n=k+1时左端在n=k时的左端加上________.
 时,第一步验证
时,第一步验证 时,左边应取的项是( )
时,左边应取的项是( ) 、
、 、
、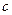 为实数,
为实数, ,则下列四个结论中正确的是( )
,则下列四个结论中正确的是( )


