题目内容
平面内有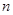 条直线,其中任何两条不平行,任何三条不共点,当
条直线,其中任何两条不平行,任何三条不共点,当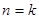 时把平面分成的区域数记为
时把平面分成的区域数记为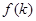 ,则
,则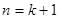 时
时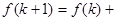 .
.
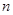 条直线,其中任何两条不平行,任何三条不共点,当
条直线,其中任何两条不平行,任何三条不共点,当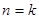 时把平面分成的区域数记为
时把平面分成的区域数记为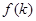 ,则
,则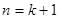 时
时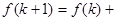 .
.k
试题分析:当
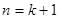 时,任取其中1条直线,记为
时,任取其中1条直线,记为 ,则除
,则除 外的其他k条直线的交点的个数为
外的其他k条直线的交点的个数为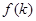 ,因为已知任何两条直线不平行,所以直线
,因为已知任何两条直线不平行,所以直线 必与平面内其他k条直线都相交(有k个交点);
必与平面内其他k条直线都相交(有k个交点);又因为已知任何三条直线不过同一点,所以上面的k个交点两两不相同,且与平面内其他的f(k)个交点也两两不相同,从而平面内交点的个数是
 .故:
.故: .
.
练习册系列答案
相关题目
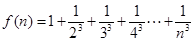 ,
, ,
,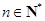 .
.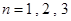 时,试比较
时,试比较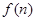 与
与 的大小关系;
的大小关系;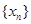 对一切
对一切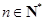 均满足
均满足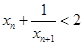 .证明:
.证明: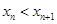 ;
;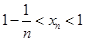 .
.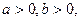 求证
求证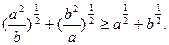
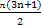 (n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .
(n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .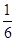 n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.