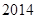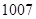题目内容
如图,在由二项式系数所构成的杨辉三角形中,
若第 行中从左至右第
行中从左至右第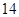 与第
与第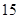 个数的比为
个数的比为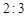 ,
,
则 的值为
的值为
A.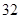 | B.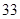 |
C.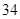 | D. |
C
解析试题分析:根据题意,由于由二项式系数所构成的杨辉三角形中,若第 行中从左至右第
行中从左至右第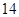 与第
与第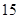 个数的比为
个数的比为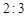 ,即可知为
,即可知为 ,则根据组合数的公式可知解得为n=34,g故答案为C.
,则根据组合数的公式可知解得为n=34,g故答案为C.
考点:数列的概念
点评:主要是考查了归纳猜想的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列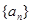 的前
的前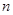 项和为
项和为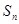 ,且
,且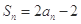 则
则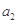 等于( )
等于( )
| A.4 | B.2 | C.1 | D.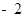 |
数列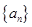 中,已知对任意正整数
中,已知对任意正整数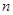 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
如果数列 的前
的前 项和
项和 ,那么这个数列的通项公式是 ( )
,那么这个数列的通项公式是 ( )
A. | B. |
C. | D.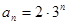 |
已知数列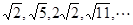 ,则
,则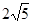 是这个数列的 ( )
是这个数列的 ( )
A.第 项 项 | B.第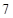 项 项 | C.第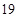 项 项 | D.第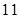 项 项 |
在各项均为正数的数列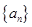 中,对任意
中,对任意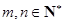 都有
都有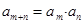 .若
.若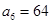 ,
,
则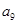 等于( )
等于( )
| A.256 | B.510 | C.512 | D.1024 |
、数列{an}、{bn}的通项公式分别是an="an+b" (a≠0,a、b∈R),bn=qn-1(q>1),则数列{an}、{bn}中,使an=bn的n值的个数是( )
| A.2 | B.1 |
| C.0 | D.可能为0,可能为1,可能为2 |
 ,点
,点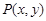 为直线
为直线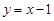 上的一个动点.
上的一个动点. 恒为锐角;
恒为锐角; 为菱形,求
为菱形,求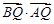 的值.
的值. 中,对任意正整数
中,对任意正整数 ,都有
,都有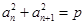 (常数),则称数列
(常数),则称数列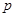 为“公方和”,若数列
为“公方和”,若数列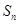 ,且“公方和”为
,且“公方和”为 ,首项
,首项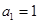 ,则
,则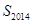 的最大值与最小值之和为( )
的最大值与最小值之和为( )