题目内容
如果数列 的前
的前 项和
项和 ,那么这个数列的通项公式是 ( )
,那么这个数列的通项公式是 ( )
A. | B. |
C. | D.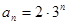 |
D
解析试题分析: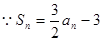 ,
,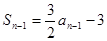 ,
,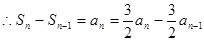 ,即:
,即: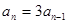
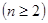 .
.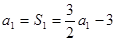 ,解得:
,解得: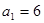 ,故
,故 是以
是以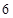 为首项,公比为
为首项,公比为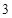 的等比数列,所以
的等比数列,所以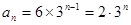
故选D.
考点:数列的通项公式的求法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列{an}满足an = nkn(n∈N*,0 < k < 1),下面说法正确的是( )
①当 时,数列{an}为递减数列;
时,数列{an}为递减数列;
②当 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;
③当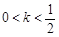 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当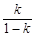 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.
| A.①② | B.②④ | C.③④ | D.②③ |
数列 ,3,
,3, ,
, ,
, ,…,则9是这个数列的第( )
,…,则9是这个数列的第( )
| A.12项 | B.13项 | C.14项 | D.15项 |
数列 中的
中的 一个值等于
一个值等于
A. | B. | C. | D. |
已知数列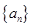 ,
, ,
, ,且
,且 ,则数列的第五项为( )
,则数列的第五项为( )
A. | B. | C. | D. |
数列1,2,4,8,16,32,…的一个通项公式是( )
| A.an=2n-1 | B.an= | C.an= | D.an= |
 +
+ +
+ =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形. 行中从左至右第
行中从左至右第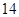 与第
与第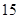 个数的比为
个数的比为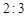 ,
,
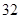
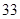
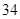


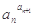 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )