题目内容
、数列{an}、{bn}的通项公式分别是an="an+b" (a≠0,a、b∈R),bn=qn-1(q>1),则数列{an}、{bn}中,使an=bn的n值的个数是( )
| A.2 | B.1 |
| C.0 | D.可能为0,可能为1,可能为2 |
D
解析

练习册系列答案
相关题目
数列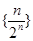 的前
的前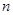 项的和为
项的和为
A.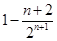 | B.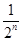 |
C.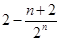 | D.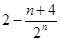 |
在数列-1,0, ,
, ,……,
,……, 中,0.08是它的( )
中,0.08是它的( )
| A.第100项 | B.第12项 | C.第10项 | D.第8项 |
.定义:在数列{an}中,an>0且an≠1,若
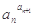 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
| A.6026 | B.6024 | C.2 | D.4 |
数列1,-3,5,-7,9,…的一个通项公式为 ( )
A. | B. |
C. | D. |
 行中从左至右第
行中从左至右第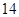 与第
与第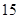 个数的比为
个数的比为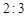 ,
,
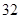
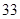
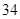

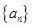 的首项
的首项 ,其前
,其前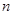 项和为
项和为 ,且满足
,且满足 .若对任意的
.若对任意的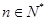 ,
, 恒成立,则
恒成立,则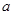 的取值范围是 .
的取值范围是 .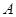 和一个运算出口
和一个运算出口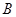 ,执行某种运算程序.
,执行某种运算程序. 时,从
时,从 ,记为
,记为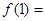
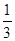 ;
;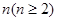 时,在
时,在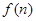 是前一结果
是前一结果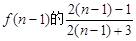 倍.
倍.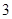 时,从
时,从 ,则应从
,则应从 中,
中, 则通项
则通项 ____________.
____________.