题目内容
若在数列 中,对任意正整数
中,对任意正整数 ,都有
,都有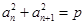 (常数),则称数列
(常数),则称数列 为“等方和数列”,称
为“等方和数列”,称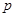 为“公方和”,若数列
为“公方和”,若数列 为“等方和数列”,其前
为“等方和数列”,其前 项和为
项和为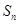 ,且“公方和”为
,且“公方和”为 ,首项
,首项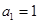 ,则
,则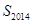 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A.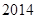 | B.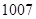 | C. | D. |

解析试题分析:由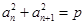 得
得 ,两等式相减得:
,两等式相减得: .又“公方和”为
.又“公方和”为 ,首项
,首项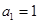 ,所以
,所以 .所以
.所以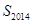 的最大值为1007,最小值为1005,其差为2.选D.
的最大值为1007,最小值为1005,其差为2.选D.
考点:1、新定义;2、数列.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知向量a=(1,2),b=(-2,m),x=a+(t2+1)b,y=-ka+ b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.
(1)若a∥b,求m的值;
(2)若a⊥b,求m的值;
(3)当m=1时,若x⊥y,求k的最小值.
已知数列:2,0,2,0,2,0, .前六项不适合下列哪个通项公式
A. =1+(―1)n+1 =1+(―1)n+1 | B. =2|sin =2|sin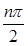 | | |
C. =1-(―1)n =1-(―1)n | D. =2sin =2sin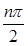 |
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
用火柴棒摆“金鱼”,如图所示: 
按照上面的规律,第 个“金鱼”图需要火柴棒的根数为( )
个“金鱼”图需要火柴棒的根数为( )
A. | B. | C. | D. |
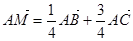 ,则
,则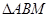 与
与 的面积之比为 .
的面积之比为 . 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为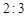 ,
,
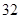
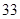
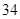

 个点,相应的图案中总的点数记为
个点,相应的图案中总的点数记为 ,则
,则 +
+ +
+ + …… +
+ …… + =( )
=( )




 中,
中, 则通项
则通项 ____________.
____________.