题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，且
=
．
（1）求角A的值；
（2）若∠B=
，BC边上中线AM=
，求△ABC的面积．
2b-
| ||
|
| cosC |
| cosA |
（1）求角A的值；
（2）若∠B=
| π |
| 6 |
| 7 |
考点：正弦定理
专题：计算题,解三角形
分析：（1）利用正弦定理化边为角可求得cosA=
，从而可得A；
（2）易求角C，可知△ABC为等腰三角形，在△AMC中利用余弦定理可求b，再由三角形面积公式可求结果；
| ||
| 2 |
（2）易求角C，可知△ABC为等腰三角形，在△AMC中利用余弦定理可求b，再由三角形面积公式可求结果；
解答：
解：（1）∵
=
．
∴由正弦定理，得
=
，化简得cosA=
，
∴A=
；
（2）∵∠B=
，∴C=π-A-B=
，
可知△ABC为等腰三角形，
在△AMC中，由余弦定理，得AM2=AC2+MC2-2AC•MCcos120°，即7=b2+(
)2-2×b×
×cos120°，
解得b=2，
∴△ABC的面积S=
b2sinC=
×22×
=
．
2b-
| ||
|
| cosC |
| cosA |
∴由正弦定理，得
2sinB-
| ||
|
| cosC |
| cosA |
| ||
| 2 |
∴A=
| π |
| 6 |
（2）∵∠B=
| π |
| 6 |
| 2π |
| 3 |
可知△ABC为等腰三角形，
在△AMC中，由余弦定理，得AM2=AC2+MC2-2AC•MCcos120°，即7=b2+(
| b |
| 2 |
| b |
| 2 |
解得b=2，
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评：该题考查正弦定理、余弦定理及三角形的面积公式，属基础题，熟记相关公式并灵活运用是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
a=log9
，b=log8
，c=
，则a，b，c的大小关系是（ ）
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、a＞c＞b |
| D、b＞c＞a |
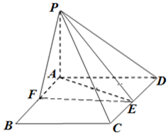如图，P-AD-C是直二面角，四边形ABCD为菱形，且∠BAD=120°，AB=2，PA⊥AD，E是CD的中点，设PC与平面ABCD所成的角为45°．