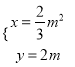题目内容
【题目】已知双曲线C： 
=1的离心率为 
，点（ ，0）是双曲线的一个顶点．
（1）求双曲线的方程；
（2）经过的双曲线右焦点F2作倾斜角为30°直线l，直线l与双曲线交于不同的A，B两点，求AB的长．
【答案】
（1）解：∵双曲线C： 
=1的离心率为 
，
点（ ，0）是双曲线的一个顶点，
∴ 
，解得c=3，b= 
，
∴双曲线的方程为 
．
（2）解：双曲线 的右焦点为F2（3，0），
∴经过的双曲线右焦点F2作倾斜角为30°直线l的方程为y= 
（x﹣3），
联立 
，得5x2+6x﹣27=0，
设A（x1，y1），B（x2，y2），则 
， 
，
|AB|= 
= 
．
【解析】（1）由已知得 ，由此能求出双曲线的方程．（2）直线l的方程为y= （x﹣3），联立 ，得5x2+6x﹣27=0，由此能求出|AB|．
练习册系列答案
相关题目
【题目】某淘宝店经过对春节七天假期的消费者进行统计，发现在金额不超过1000元的消费者中男女比例为
，该店按此比例抽取了100名消费者进行进一步分析，得到下表女性消费情况：
消费金额(元) |
|
|
|
|
|
人数 | 5 | 10 | 15 | 47 | 3 |
男性消费情况：
消费金额(元) |
|
|
|
|
|
人数 | 2 | 3 | 10 | 3 | 2 |
若消费金额不低于600元的网购者为“网购达人”，低于600元的网购者为“非网购达人”
(1)分别计算女性和男性消费的平均数，并判断平均消费水平高的一方“网购达人”出手是否更阔绰？
(2)根据以上统计数据填写如下
列联表，并回答能否在犯错误的概率不超过
的前提下认为“是否为‘网购达人’与性别有关”.
女性 | 男性 | 合计 | |
“网购达人” | |||
“非网购达人” | |||
合计 |
附： 
.
|
|
|
|
|
|
|
|
|
|
|
|
