题目内容
函数f(x)=3ax+1-2a在(-1,1)上存在x0,使f(x0)=0,则a的取值范围是( )
A.-1<a<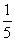 B.a>
B.a>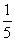
C.a<-1或a>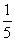 D.a<-1
D.a<-1
C
[分析] a≠0时,f(x)为一次函数,故由x0∈(-1,1)时,f(x0)=0知,f(-1)与f(1)异号.
[解析] 由题意得f(-1)·f(1)<0,
即(-3a+1-2a)·(3a+1-2a)<0,
即(5a-1)(a+1)>0,∴a<-1或a>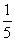 .故选C.
.故选C.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
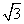 ,则c:sinC等于( )
,则c:sinC等于( )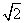 :1 D.2;1
:1 D.2;1 下,目标函数z=x+5y的最大值为4,则m的值为________.
下,目标函数z=x+5y的最大值为4,则m的值为________. B.1+2
B.1+2
 <1的解集为{x|x<1或x>2},则实数a=____________.
<1的解集为{x|x<1或x>2},则实数a=____________.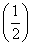 =
= .
.