题目内容
若关于x的不等式2x2+ax-a2>0的解集中的一个元素为1,则实数a的取值范围是( )
| A、(-∞,-1)∪(2,+∞) | ||
| B、(-1,2) | ||
C、(-∞,-1)∪(
| ||
D、(-1,
|
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:把1代入得到关于a的不等式,解得即可
解答:
解:关于x的不等式2x2+ax-a2>0的解集中的一个元素为1;
∴2+a-a2>0,
即(a-2)(a+1)<0,
解得-1<a<2,
故选B.
∴2+a-a2>0,
即(a-2)(a+1)<0,
解得-1<a<2,
故选B.
点评:本题考查了不等式的解法及不等式的解集有一个元素的判断,属于基础题

练习册系列答案
相关题目
已知集合A={-1,2},B={x|mx+1=0},若A∩B=B,则所有实数m的值组成的集合是( )
| A、{-1,2} | ||
B、{1,-
| ||
C、{1,0,-
| ||
D、{-1,0,
|
函数y=10|x+1|-1的单调减区间为( )
| A、(-∞,-1) |
| B、(-∞,1) |
| C、(-1,+∞) |
| D、(1,+∞) |
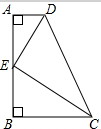 如图,在直角梯形ABCD中,AB⊥AD,AB⊥BC,∠BCD与∠ADC的平分线相交于AB上的一点E,以AB为直径作圆,则该圆与边DC有怎样的位置关系?请说明理由.
如图,在直角梯形ABCD中,AB⊥AD,AB⊥BC,∠BCD与∠ADC的平分线相交于AB上的一点E,以AB为直径作圆,则该圆与边DC有怎样的位置关系?请说明理由.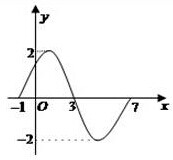 如图为函数y1=Asin(ωx+φ)(|φ|<
如图为函数y1=Asin(ωx+φ)(|φ|<